题目内容
已知圆x2+y2-4ax+2ay+20(a-1)=0.
(1)求证对任意实数a,该圆恒过一定点;
(2)若该圆与圆x2+y2=4相切,求a的值
(1)求证对任意实数a,该圆恒过一定点;
(2)若该圆与圆x2+y2=4相切,求a的值
(1)将圆的方程整理为(x2+y2-20)+a(-4x+2y+20)=0,令可得所以该圆恒过定点(4,-2).
(2)圆的方程可化为(x-2a)2+(y+a)2=5a2-20a+20
=5(a-2)2,所以圆心为(2a,a),半径为|a-2|.
若两圆外切,则=2+|a-2|,
即|a|=2+|a-2|,由此解得a=1+.
若两圆内切,则=|2-|a-2||,即|a|=|2-|a-2||,由此解得a=1-或a=1+(舍去).
综上所述,两圆相切时,a=1-或a=1+
(2)圆的方程可化为(x-2a)2+(y+a)2=5a2-20a+20
=5(a-2)2,所以圆心为(2a,a),半径为|a-2|.
若两圆外切,则=2+|a-2|,
即|a|=2+|a-2|,由此解得a=1+.
若两圆内切,则=|2-|a-2||,即|a|=|2-|a-2||,由此解得a=1-或a=1+(舍去).
综上所述,两圆相切时,a=1-或a=1+
略

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
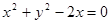 和
和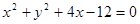 的位置关系是( )
的位置关系是( )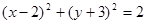 的圆心和半径分别是 ( )
的圆心和半径分别是 ( )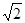
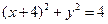 ,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点
,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点 P(-3,
P(-3, 0)
0) (0,3),求
(0,3),求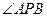 的正切值;
的正切值;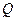 ,当圆D在y轴上运动时,
,当圆D在y轴上运动时,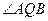 是定值?如果存在,求点
是定值?如果存在,求点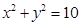 和
和 相交于
相交于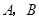 两点,则直线
两点,则直线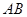 的方程是 .
的方程是 .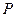 在圆
在圆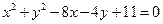 上运动,点
上运动,点 在圆
在圆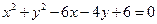 上运动,则
上运动,则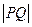 的最小值为 .
的最小值为 .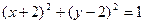 与圆C2:
与圆C2: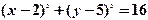 的位置关系是( )
的位置关系是( )