题目内容
(1)求证:2n+2·3n+5n-4能被25整除;
(2)求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).
(2)求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).
(1)见解析 (2)见解析
证明:(1)原式=4(5+1)n+5n-4
=4(C n05n+C n15n-1+Cn25n-2+…+Cnn)+5n-4
=4(C n05n+C n15n-1+…+C nn-2·52+C nn-1·51+1)+5n-4
=4(C n05n+C n15n-1+…+C nn-2·52)+25n,
以上各项均为25的整数倍,故得证.
(2)因为1+3+32+…+33n-1=
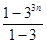 =
=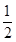 (33n-1)
(33n-1)=
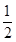 (27n-1)=
(27n-1)=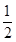 [(26+1)n-1].
[(26+1)n-1].而(26+1)n-1=C n026n+C n126n-1+…+C nn-126+Cnn260-1
=Cn026n+Cn126n-1+…+Cnn-126
因为n为大于1的偶数,所以原式能被26整除.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
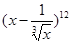 展开式中的常数项为( )
展开式中的常数项为( )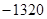
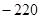
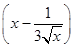 18的展开式中含x15的项的系数为________(结果用数值表示).
18的展开式中含x15的项的系数为________(结果用数值表示).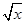 )8展开式中不含x4项的系数的和为________.
)8展开式中不含x4项的系数的和为________. ,则二项式
,则二项式 的展开式中含有
的展开式中含有 的项是 .
的项是 .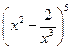 展开式中的常数项为( )
展开式中的常数项为( ) +
+ +…+
+…+ 的值为( )
的值为( )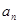 是
是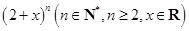 展开式中
展开式中 项的系数,
项的系数, .
.