题目内容
已知椭圆 的离心率
的离心率 ,且椭圆过点
,且椭圆过点 .
.
(1)求椭圆 的方程;
的方程;
(2)若 为椭圆
为椭圆 上的动点,
上的动点, 为椭圆的右焦点,以
为椭圆的右焦点,以 为圆心,
为圆心, 长为半径作圆
长为半径作圆 ,过点
,过点 作圆
作圆 的两条切线
的两条切线 ,(
,( 为切点),求点
为切点),求点 的坐标,使得四边形
的坐标,使得四边形 的面积最大.]
的面积最大.]
(1)依题意得,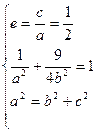 ………………………………3分
………………………………3分
解得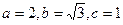 ,
, 
所以椭圆 的方程为
的方程为 . ………………………………4分
. ………………………………4分
(2)设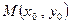 ,圆
,圆 :
: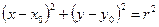 ,
,
其中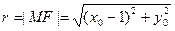
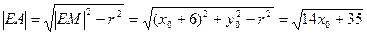 ,
, ……6分
……6分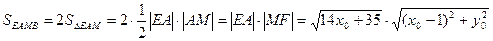 ……7分
……7分
又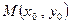 在椭圆
在椭圆 上,
上,
则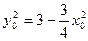
所以 ,
, ………………………8分
………………………8分
令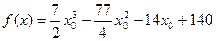 ,
,
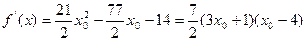 ,
, …………………9分
…………………9分
当 时,
时,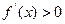 ,当
,当 时,
时, …………………10分
…………………10分
所以当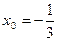 时,
时, 有最大值,
有最大值,
即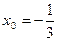 时,四边形
时,四边形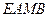 面积取得最大值…11分
面积取得最大值…11分
此时点 的坐标为
的坐标为 或
或 …………………………12分
…………………………12分
解析

练习册系列答案
相关题目
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
| A.θ=0(ρ∈R)和ρcos θ=2 | B.θ=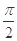 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=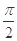 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 | D.θ=0(ρ∈R)和ρcos θ=1 |
在极坐标系中,直线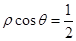 与曲线
与曲线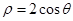 相交于
相交于 两点,
两点,  为极点,则
为极点,则 的大小为( ).
的大小为( ).
A.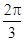 | B.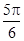 | C.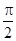 | D.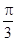 |
在极坐标系中,圆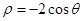 的圆心的极坐标为( )
的圆心的极坐标为( )
A.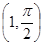 | B. | C. | D.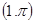 |
在极坐标系中,圆 的垂直于极轴的两条切线方程分别为( )
的垂直于极轴的两条切线方程分别为( )
A. | B. |
C. | D. |
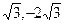 ),
),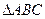 的两个顶点
的两个顶点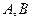 的坐标分别为
的坐标分别为 ,平面内两点
,平面内两点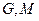 同时满足一下条件:①
同时满足一下条件:①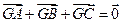 ;②
;②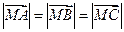 ;③
;③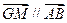
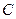 的轨迹方程;
的轨迹方程;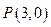 的直线
的直线 与(1)中的轨迹交于
与(1)中的轨迹交于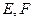 两点,求
两点,求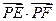 的取值范围。
的取值范围。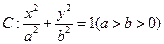 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为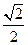 。过点M作倾斜角
。过点M作倾斜角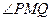 能否为直角?证明你的结论;
能否为直角?证明你的结论; 求这个定值。
求这个定值。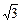 ,求椭圆的方程.
,求椭圆的方程.