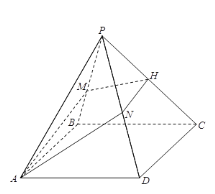
题目内容
【题目】函数![]() ,其中
,其中![]() ,
,![]() ,为实常数
,为实常数
(1)若![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)若![]() 时,不等式
时,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,当
,当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)见解析;(2) ![]() (3)见证明
(3)见证明
【解析】
(1)代入t的值,求得导函数,对a进行分类讨论,根据导数的正负确定单调区间即可.
(2)代入t的值,根据不等式分离参数,通过构造函数![]() ,再求
,再求![]() ,根据其单调性求得最大值即可得a的取值范围.
,根据其单调性求得最大值即可得a的取值范围.
(3)要证明不等式成立,根据分析法得到只需证明![]() 成立即可.通过构造函数
成立即可.通过构造函数![]() ,利用导数研究其单调性与最值,根据最小值即可得证.
,利用导数研究其单调性与最值,根据最小值即可得证.
解(1)定义域为![]() ,
,![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]()
![]() ,
,
![]() 在定义域
在定义域![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() .
.![]() 单调递减;
单调递减;
综上可知:当![]() 时,
时,![]() 的增区间为
的增区间为![]() ,无减区间;
,无减区间;
当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;
;
(2)![]()
![]()
![]()
![]() 对任意
对任意![]() 恒成立.
恒成立.
即等价于![]() ,
,![]() ,
,
令![]() .
.
![]()
![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() .故
.故![]() 的取值范围为
的取值范围为![]() .
.
(3)要证明![]() ,即证明
,即证明![]() ,只要证
,只要证![]() ,
,
即证![]() ,只要证明
,只要证明![]() 即可,
即可,
令![]() ,
,![]() 在
在![]() 上是单调递增,
上是单调递增,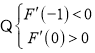 ,
,
![]() 在
在![]() 有唯一实根设为
有唯一实根设为![]() ,
,
且![]() ,
,
当![]() 时
时![]() ,
,![]() 单调递减
单调递减
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
从而当![]() 时,
时,![]() 取得最小值,由
取得最小值,由![]() 得:
得:
![]() ,即
,即![]() ,
,
![]()
![]()
![]()
 ,
,
故当![]() 时,证得:
时,证得:![]() .
.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分![]() 市某调查机构针对该市市场占有率最高的两种网络外卖企业
市某调查机构针对该市市场占有率最高的两种网络外卖企业![]() 以下简称外卖A、外卖
以下简称外卖A、外卖![]() 的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
分数 人数 种类 |
|
|
|
|
|
外卖A | 50 | 150 | 100 | 400 | 300 |
外卖B | 100 | 100 | 300 | 200 | 300 |
表中得分越高,说明市民对网络外卖服务越满意![]() 若得分不低于60分,则表明该市民对网络外卖服务质量评价较高
若得分不低于60分,则表明该市民对网络外卖服务质量评价较高![]() 现将分数按“服务质量指标”划分成以下四个档次:
现将分数按“服务质量指标”划分成以下四个档次:
分数 |
|
|
|
|
服务质量指标 | 0 | 1 | 2 | 3 |
视频率为概率,解决下列问题:
![]() 从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
![]() 从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
![]() 在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.