题目内容
17．已知集合A={y|y=x2+4x-1}，B={x|y2=-2x+3}，求A∪B，A∩B．分析 分别求解函数的值域及x的取值范围化简集合A，B，然后利用交集、并集运算得答案．
解答 解：∵y=x2+4x-1=（x+2）2-5≥-5，
∴A={y|y=x2+4x-1}=[-5，+∞）；
由y2=-2x+3，得-2x=y2-3，∴-2x≥-3，$x≤\frac{3}{2}$．
∴B={x|y2=-2x+3}=（-∞，$\frac{3}{2}$]．
则A∪B=[-5，+∞）∪（-∞，$\frac{3}{2}$]=R；
A∩B=[-5，+∞）∩（-∞，$\frac{3}{2}$]=[-5，$\frac{3}{2}$]．
点评 本题考查交集、并集及其运算，考查了函数定义域的求法，是基础题．
练习册系列答案
相关题目
8．sin（-1050°）=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
2．
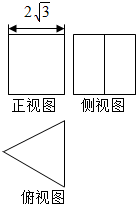一个体积为12$\sqrt{3}$的正三棱柱（底面为正三角形，且侧棱垂直于底面的棱柱）的三视图如图所示，则该三棱柱的侧视图的面积为（ ）
一个体积为12$\sqrt{3}$的正三棱柱（底面为正三角形，且侧棱垂直于底面的棱柱）的三视图如图所示，则该三棱柱的侧视图的面积为（ ）| A． | 6$\sqrt{3}$ | B． | 8 | C． | 8$\sqrt{3}$ | D． | 12 |
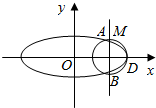已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短轴长为2，离心率e=$\frac{\sqrt{2}}{2}$．