题目内容
投掷骰子2次,记第一次掷出的点数为a,第二次掷出的点数为b,现以(a,b)表示基本事件,事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件的概率为 .
【答案】分析:事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件为“复数z1=a+bi与z2=1+2i对应的向量共线”,从而可求a,b的关系,进而可求概率.
解答:解:事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件为“复数z1=a+bi与z2=1+2i对应的向量共线”,故b=2a,基本事件为(1,2),(2,4),(3,6),又所有基本事件共有36种,故所求的概率为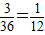 ,
,
故答案为:
点评:本题主要考查古典概型概率的求解,搞清基本事件的个数是解题的关键.
解答:解:事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件为“复数z1=a+bi与z2=1+2i对应的向量共线”,故b=2a,基本事件为(1,2),(2,4),(3,6),又所有基本事件共有36种,故所求的概率为
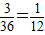 ,
,故答案为:

点评:本题主要考查古典概型概率的求解,搞清基本事件的个数是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,第二次出现的点数为
,第二次出现的点数为 (其中
(其中 ).
). “焦点在
“焦点在 轴上的椭圆的方程为
轴上的椭圆的方程为 ”,求事件
”,求事件 “离心率为2的双曲线的方程为
“离心率为2的双曲线的方程为 ”,求事件
”,求事件