题目内容
某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?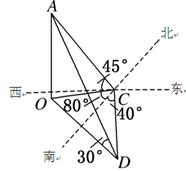
h=10,或h=-5(舍).
解析试题分析:如图,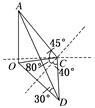
设塔高为h,在Rt△AOC中,∠ACO=45°,则OC=OA=h.…(2分)在Rt△AOD中,∠ADO=30°,则OD=h, (4分)
在△OCD中,∠OCD=120°,CD=10,由余弦定理得:OD2=OC2+CD2-2OC·CDcos∠OCD,即(h)2=h2+102-2h×10×cos120° (8分),
∴h2-5h-50=0,解得h=10,或h=-5(舍). 12分
考点:正弦定理、余弦定理的应用。
点评:典型题,本题综合考查正弦定理、余弦定理的应用,本题解答结合图形,在不同的几个三角形中,灵活运用正弦定理或余弦定理,反映应用数学知识的灵活性。解决“追击问题”,测量高度或距离问题,准确绘制几何图形,明确边、角,是解题的关键。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,且
,且
 且
且 ,求
,求 的取值范围.
的取值范围. 
 的最小正周期和值域;
的最小正周期和值域; 的内角A、B、C的对边分别是a,b,c,若
的内角A、B、C的对边分别是a,b,c,若 求角C的值。
求角C的值。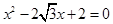 的两个根,且
的两个根,且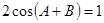 。求:⑴ 角C的度数; ⑵ AB的长度。
。求:⑴ 角C的度数; ⑵ AB的长度。 中,角
中,角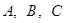 所对的边分别为
所对的边分别为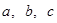 且满足
且满足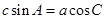 .
.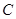 的大小; (2)求
的大小; (2)求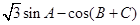 的取值范围.
的取值范围.  且
且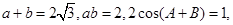
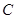 度数 (2)
度数 (2) 的长 (3)△ABC的面积
的长 (3)△ABC的面积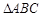 中,已知
中,已知 求∠A,∠C,边c.
求∠A,∠C,边c.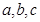 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且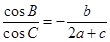
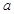 =4,
=4,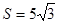 ,求
,求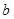 的值。
的值。 中,已知
中,已知 ,
, ,
, , 求
, 求 、
、 及
及 。
。