题目内容
13.数列{logkan}是首项为4,公差为2的等差数列,其中k>0,且k≠1,设cn=anlgan,若{cn}中的每一项恒小于它后面的项,则实数k的取值范围为$(0,\frac{\sqrt{6}}{3})$∪(1,+∞).分析 利用等差数列的通项公式可得:logkan=2n+2,解出an=k2n+2.可得$\frac{{a}_{n+1}}{{a}_{n}}$=k2.可得cn=anlgan=(2n+2)•k2n+2lgk.要使cn<cn+1对?n∈N*恒成立,化为:(n+1)lgk<(n+2)•k2•lgk.对k分类讨论即可得出.
解答 解:∵logkan=4+2(n-1)=2n+2,∴an=k2n+2.
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{k}^{2(k+1)+2}}{{k}^{2n+2}}$=k2.
∴数列{an}是等比数列,首项为k4,公比为k2.
∴cn=anlgan=(2n+2)•k2n+2lgk.
要使cn<cn+1对?n∈N*恒成立,∴(2n+2)•k2n+2lgk<(2n+4)k2n+4•lgk,化为:(n+1)lgk<(n+2)•k2•lgk.
当k>1时,lgk>0,化为:(n+1)<(n+2)•k2.此式恒成立.
当0<k<1时,lgk<0,化为:(n+1)>(n+2)•k2.对n∈N*恒成立,只需k2<$(\frac{n+1}{n+2})_{min}$,
∵$\frac{n+1}{n+2}$=1-$\frac{1}{n+2}$单调递增,∴当n=1时,$(\frac{n+1}{n+2})_{min}$=$\frac{2}{3}$.
∴k2$<\frac{2}{3}$,且0<k<1,∴$0<k<\frac{\sqrt{6}}{3}$.
综上可得:$(0,\frac{\sqrt{6}}{3})$∪(1,+∞).
故答案为:$(0,\frac{\sqrt{6}}{3})$∪(1,+∞).
点评 本题考查了数列的单调性、等比数列的通项公式、对数的运算性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.

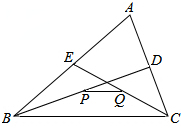
| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
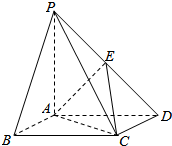 如图,在底面是菱形的四棱锥P-ABCD中∠ABC=60°,PA=AC=1,PB=PD=$\sqrt{2}$,若E是侧棱PD的中点
如图,在底面是菱形的四棱锥P-ABCD中∠ABC=60°,PA=AC=1,PB=PD=$\sqrt{2}$,若E是侧棱PD的中点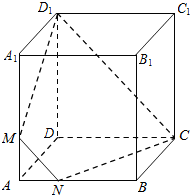 如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上
如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上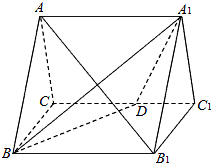 如图,正三棱柱ABC-A1B1C1的所有棱长都为4,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为4,D为CC1中点.