题目内容
18.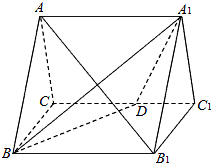 如图,正三棱柱ABC-A1B1C1的所有棱长都为4,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为4,D为CC1中点.(Ⅰ)求证:AB1⊥平面A1BD;
(Ⅱ)求直线AB1与平面BCC1B1所成角的正弦值.
分析 (Ⅰ)取BC中点O,连结AO,B1O,由已知得AO⊥BC,从而AO⊥面BCC1B1,再推财导出BD⊥AO,BD⊥B1O,从而得到AB1⊥BD,由正方形性质得BD⊥B1O,由此能证明AB1⊥平面A1BD.
(Ⅱ)由AO⊥平面BCC1B1,得∠AB1O是直线AB1与平面BCC1B1所成的角,由此能求出直线AB1与平面BCC1B1所成角的正弦值.
解答 证明:(Ⅰ)如图,取BC中点O,连结AO,B1O,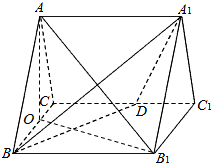
∵△ABC为正三角形,∴AO⊥BC,
∵正三角形ABC-A1B1C1中,平面ABC⊥平面BCC1B1,
且面ABC∩面BCC1B1=BC,∴AO⊥面BCC1B1,
∵BD?面BCC1B1,∴BD⊥AO,
在正方形BB1C1C中,O,D分别为BC、CC1的中点,∴BD⊥B1O,
∵AO∩B1O=O,AO、B1O?面AB1O,∴BD⊥面AB1O,
又AB1?面AB1O,∴AB1⊥BD,
在正方形BB1C1C中,O、D分别为BC、CC1的中点,∴BD⊥B1O,
∵AO∩B1O=O,AO,B1O?面AB1O,∴BD⊥面AB1O,
又AB1?面AB1O,∴AB1⊥BD,
又BD∩A1B=B,AB1⊥平面A1BD.
解:(Ⅱ)由(Ⅰ)知,AO⊥平面BCC1B1,
∴OB1是直线AB1在平面BCC1B1内的射影,
∴∠AB1O是直线AB1与平面BCC1B1所成的角,
∵AO=$\sqrt{A{B}^{2}-(\frac{BC}{2})^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
AB1=$\sqrt{A{B}^{2}+B{{B}_{1}}^{2}}$=4$\sqrt{2}$,
∴sin∠AB1O=$\frac{AO}{A{B}_{1}}$=$\frac{2\sqrt{3}}{4\sqrt{2}}$=$\frac{\sqrt{6}}{4}$,
∴直线AB1与平面BCC1B1所成角的正弦值为$\frac{\sqrt{6}}{4}$.
点评 本查线面垂直的证明,考查线面角的正弦值的求法,是中档题,解题时要注意空间思维能力的培养.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (0,$\frac{\sqrt{6}}{3}$) | B. | ($\frac{\sqrt{6}}{3}$,1) | C. | (0,$\sqrt{3}$-1) | D. | ($\sqrt{3}$-1,1) |
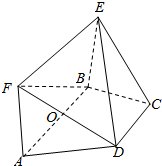 如图,几何体ABCDEF中,四边形ABEF为矩形,ABCD为梯形,平面ABEF⊥平面ABCD,AB∥CD,AB=4,AF=AD=CD=2,AD⊥BD,O为AB的中点.
如图,几何体ABCDEF中,四边形ABEF为矩形,ABCD为梯形,平面ABEF⊥平面ABCD,AB∥CD,AB=4,AF=AD=CD=2,AD⊥BD,O为AB的中点.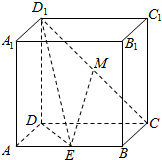 在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2,点E是线段AB的中点,点M为线段D1C上的动点.,
在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2,点E是线段AB的中点,点M为线段D1C上的动点.,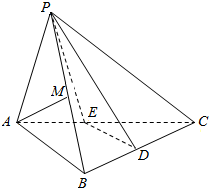 如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.