题目内容

某同学为了研究学生的性别与是否支持某项活动的关系，运用2×2列联表进行独立性检验，已知样本的观测值K²=7.28，临界值如下表所示：

P（K²≥k₀）	0.1	0.05	0.025	0.01	0.005	0.001
k₀	2.706	3.841	5.024	6.635	7.897	10.828

则有多大把握认为“学生的性别与支持这项活动有关系”（　　）

A、99.9%	B、99.5%
C、99.3%	D、99%

分析：对照临界值表，即可得出结论．

解答：解：∵K²=7.28＞6.635，
对照临界值表：

P（k²≥k₀）	0.100	0.050	0.025	0.010	0.001
k₀	2.706	3.841	5.024	6.635	10.828

∴有99%的把握认为“学生的性别与支持这项活动有关系”．
故选：D．

点评：本题考查独立性检验知识的运用，正确对照临界值表是关键．

练习册系列答案

复习计划风向标暑系列答案

开心快乐假期作业暑假作业西安出版社系列答案

学业考试综合练习册系列答案

名题训练系列答案

全品中考试卷系列答案

全效系列丛书赢在期末系列答案

新天地期末系列答案

期末集结号系列答案

全优达标测试卷系列答案

中考必备6加14系列答案

相关题目

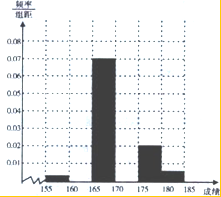某校为了解高三学生的情况，现从期末文综考试成绩中随机抽取100名学生，按成绩分组，得到的频率分布表如图：

组别	分组	频数	频率
1	[155，160]	2	0.020
2	[155，160]	①	0.300
3	[155，160]	35	0.350
4	[155，160]	20	0.200
5	[155，160]	10	②
6	[155，160]	3	0.030
合计		100	1.00

（1）请求出频率分布表中①、②位置相应的数据，并补全频率分布直方图；
（2）若在第4、5组的30人中，用分层抽样抽取6名学生参加体育测试，请问：在第4、5组各抽取多少名学生参加测试？
（3）为了进一步获得研究资料，学校决定在第1组和第6组的学生中，随机抽取3名学生进行心理测试，求第1组中的A同学和第6组中的C同学被同时抽到的概率．

有甲乙两个学校进行了一门课程的考试，某同学为了研究成绩与学校是否有关，他进行了如下实验：先将甲校和乙校各300名同学编成1～300号，然后用系统抽样的方法各抽取了20名同学（两校学生抽取号码相同），记录下他们的成绩如下表，表格中部分编号用“×”代替，空缺编号需补充．

编号		18		48		78			123
甲校	75	92	68	92	95	86	75	88	78	45
乙校	92	62	66	77	83	65	77	62	56	82
编号	×	×	×	×	×	×	×	×	×	×
甲校	86	77	85	56	82	77	86	78	88	78
乙校	78	85	66	56	55	91	65	77	79	65

（1）把表格中空白处的编号补充完整．
（2）若规定该课程分数在80分以上为“优秀”，80分以下为“非优秀”
（Ⅰ）从乙校成绩为“优秀”的学生中随机抽取2人，求两人的分数都不高于90分的概率．
（Ⅱ）试分析有多大把握认为“成绩与学校有关系”．

有甲乙两个学校进行了一门课程的考试，某同学为了研究成绩与学校是否有关，他进行了如下实验：先将甲校和乙校各300名同学编成1～300号，然后用系统抽样的方法各抽取了20名同学（两校学生抽取号码相同），记录下他们的成绩如下表，表格中部分编号用“×”代替，空缺编号需补充．
编号 18 48 78 123
甲校 75 92 68 92 95 86 75 88 78 45
乙校 92 62 66 77 83 65 77 62 56 82
编号 × × × × × × × × × ×
甲校 86 77 85 56 82 77 86 78 88 78
乙校 78 85 66 56 55 91 65 77 79 65
（1）把表格中空白处的编号补充完整．
（2）若规定该课程分数在80分以上为“优秀”，80分以下为“非优秀”
（Ⅰ）从乙校成绩为“优秀”的学生中随机抽取2人，求两人的分数都不高于90分的概率．
（Ⅱ）试分析有多大把握认为“成绩与学校有关系”．

有甲乙两个学校进行了一门课程的考试，某同学为了研究成绩与学校是否有关，他进行了如下实验：先将甲校和乙校各300名同学编成1～300号，然后用系统抽样的方法各抽取了20名同学（两校学生抽取号码相同），记录下他们的成绩如下表，表格中部分编号用“×”代替，空缺编号需补充．

编号		18		48		78			123
甲校	75	92	68	92	95	86	75	88	78	45
乙校	92	62	66	77	83	65	77	62	56	82
编号	×	×	×	×	×	×	×	×	×	×
甲校	86	77	85	56	82	77	86	78	88	78
乙校	78	85	66	56	55	91	65	77	79	65

（1）把表格中空白处的编号补充完整．
（2）若规定该课程分数在80分以上为“优秀”，80分以下为“非优秀”
（Ⅰ）从乙校成绩为“优秀”的学生中随机抽取2人，求两人的分数都不高于90分的概率．
（Ⅱ）试分析有多大把握认为“成绩与学校有关系”．