题目内容
有甲乙两个学校进行了一门课程的考试,某同学为了研究成绩与学校是否有关,他进行了如下实验:先将甲校和乙校各300名同学编成1~300号,然后用系统抽样的方法各抽取了20名同学(两校学生抽取号码相同),记录下他们的成绩如下表,表格中部分编号用“×”代替,空缺编号需补充.| 编号 | 18 | 48 | 78 | 123 | ||||||
| 甲校 | 75 | 92 | 68 | 92 | 95 | 86 | 75 | 88 | 78 | 45 |
| 乙校 | 92 | 62 | 66 | 77 | 83 | 65 | 77 | 62 | 56 | 82 |
| 编号 | × | × | × | × | × | × | × | × | × | × |
| 甲校 | 86 | 77 | 85 | 56 | 82 | 77 | 86 | 78 | 88 | 78 |
| 乙校 | 78 | 85 | 66 | 56 | 55 | 91 | 65 | 77 | 79 | 65 |
(2)若规定该课程分数在80分以上为“优秀”,80分以下为“非优秀”
(Ⅰ)从乙校成绩为“优秀”的学生中随机抽取2人,求两人的分数都不高于90分的概率.
(Ⅱ)试分析有多大把握认为“成绩与学校有关系”.
【答案】分析:(1)由题意知将300名同学编成1~300号,系统抽样的方法各抽取20名同学,得到在系统抽样中分段的间隔,根据间隔的大小做出要抽取得号数,即用所给的号数减去间隔数得到前一个空白.
(2)(I)由题意知本题是一个等可能事件的概率,试验发生所包含的事件是乙校“优秀”学生共有5人,从中抽取2人列出共10种,其中两人的分数都不高于90分共3种,得到概率.
(II)根据所给的数据列出列联表,根据列联表把数据代入求观测值的公式,做出观测值,同临界值进行比较,得到对应的概率,得到有1-0.15=85%的把握认为“成绩与学校有关系”.
解答:解:(1)∵将甲校和乙校各300名同学编成1~300号,然后用系统抽样的方法各抽取了20名同学,
∴在系统抽样中分段的间隔是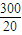 =15
=15
∴编号为:3,33,63,93,108,138 …(2分)
(2)(Ⅰ)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件是乙校“优秀”学生共有5人,从中抽取2人列出共10种,
其中两人的分数都不高于90分共3种,
所以P=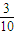 . …(7分)
. …(7分)
(II)列出成绩与学校的2×2列联表
…(9分)
∴K2=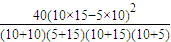 ≈2.677>2.072 …(11分)
≈2.677>2.072 …(11分)
∵P(K2=2.072)=0.15
所以有1-0.15=85%的把握认为“成绩与学校有关系”. …(12分)
点评:本题考查独立性检验的应用,考查等可能事件的概率及系统抽样,本题解题的关键是正确应用求观测值的公式,理解临界值对应的概率的意义,本题是一个综合题目.
(2)(I)由题意知本题是一个等可能事件的概率,试验发生所包含的事件是乙校“优秀”学生共有5人,从中抽取2人列出共10种,其中两人的分数都不高于90分共3种,得到概率.
(II)根据所给的数据列出列联表,根据列联表把数据代入求观测值的公式,做出观测值,同临界值进行比较,得到对应的概率,得到有1-0.15=85%的把握认为“成绩与学校有关系”.
解答:解:(1)∵将甲校和乙校各300名同学编成1~300号,然后用系统抽样的方法各抽取了20名同学,
∴在系统抽样中分段的间隔是
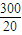 =15
=15∴编号为:3,33,63,93,108,138 …(2分)
(2)(Ⅰ)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件是乙校“优秀”学生共有5人,从中抽取2人列出共10种,
其中两人的分数都不高于90分共3种,
所以P=
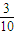 . …(7分)
. …(7分)(II)列出成绩与学校的2×2列联表
| 优秀 | 非优秀 | 总计 | |
| 甲校 | 10 | 10 | 20 |
| 乙校 | 5 | 15 | 20 |
| 总计 | 15 | 25 | 40 |
∴K2=
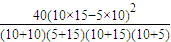 ≈2.677>2.072 …(11分)
≈2.677>2.072 …(11分)∵P(K2=2.072)=0.15
所以有1-0.15=85%的把握认为“成绩与学校有关系”. …(12分)
点评:本题考查独立性检验的应用,考查等可能事件的概率及系统抽样,本题解题的关键是正确应用求观测值的公式,理解临界值对应的概率的意义,本题是一个综合题目.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
有甲乙两个学校进行了一门课程的考试,某同学为了研究成绩与学校是否有关,他进行了如下实验:先将甲校和乙校各300名同学编成1~300号,然后用系统抽样的方法各抽取了20名同学(两校学生抽取号码相同),记录下他们的成绩如下表,表格中部分编号用“×”代替,空缺编号需补充.
| 编号 | 18 | 48 | 78 | 123 | ||||||
| 甲校 | 75 | 92 | 68 | 92 | 95 | 86 | 75 | 88 | 78 | 45 |
| 乙校 | 92 | 62 | 66 | 77 | 83 | 65 | 77 | 62 | 56 | 82 |
| 编号 | × | × | × | × | × | × | × | × | × | × |
| 甲校 | 86 | 77 | 85 | 56 | 82 | 77 | 86 | 78 | 88 | 78 |
| 乙校 | 78 | 85 | 66 | 56 | 55 | 91 | 65 | 77 | 79 | 65 |
(2)若规定该课程分数在80分以上为“优秀”,80分以下为“非优秀”
(Ⅰ)从乙校成绩为“优秀”的学生中随机抽取2人,求两人的分数都不高于90分的概率.
(Ⅱ)试分析有多大把握认为“成绩与学校有关系”.
 某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”. 某学校问了预防甲流感,每天都对同学进行体温抽查,某一天,随机抽取甲,乙两个班级各10名同学,测量他们的体温如下图(单位0.1摄氏度)
某学校问了预防甲流感,每天都对同学进行体温抽查,某一天,随机抽取甲,乙两个班级各10名同学,测量他们的体温如下图(单位0.1摄氏度)