题目内容
已知点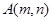 在直线
在直线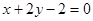 上,则
上,则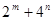 的最小值为
的最小值为
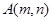 在直线
在直线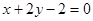 上,则
上,则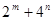 的最小值为
的最小值为 4
解:∵点A(m,n)在直线x+2y-2=0上,
∴m+2n-2=0,即 m=2-2n.
∴2m+4n=22-2n+4n =4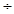 4n +4n≥2
4n +4n≥2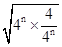 =4,当且仅当 4
=4,当且仅当 4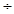 4n =4n时,等号成立,
4n =4n时,等号成立,
故2m+4n的最小值为4,
故答案为 4.
∴m+2n-2=0,即 m=2-2n.
∴2m+4n=22-2n+4n =4
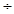 4n +4n≥2
4n +4n≥2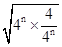 =4,当且仅当 4
=4,当且仅当 4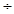 4n =4n时,等号成立,
4n =4n时,等号成立,故2m+4n的最小值为4,
故答案为 4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
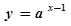 (
(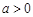 ,且
,且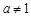 )的图象恒过定点,若点在一次函数
)的图象恒过定点,若点在一次函数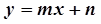 的图象上,其中
的图象上,其中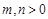 ,则
,则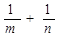 的最小值为( )
的最小值为( )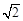
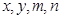 满足
满足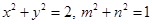 ,则
,则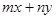 的最大值是( )
的最大值是( )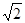
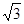
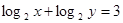 ,则
,则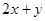 的最小值是( )
的最小值是( )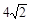
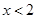 ,求:函数
,求:函数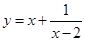 的最大值.
的最大值.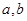 满足
满足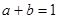 ,则( ).
,则( ).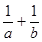 有最大值
有最大值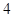
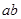 有最小值
有最小值
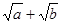 有最大值
有最大值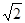
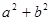 有最小值
有最小值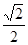
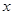 、
、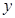 满足
满足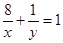 ,则
,则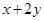 的最小值是 ( )
的最小值是 ( )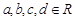 ,满足
,满足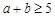 ,
, ,则有( ).
,则有( ).
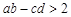
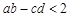
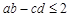
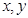 满足
满足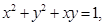 则
则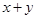 的最大值为________________.
的最大值为________________.