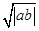题目内容
已知函数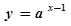 (
(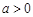 ,且
,且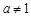 )的图象恒过定点,若点在一次函数
)的图象恒过定点,若点在一次函数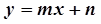 的图象上,其中
的图象上,其中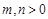 ,则
,则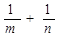 的最小值为( )
的最小值为( )
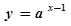 (
(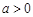 ,且
,且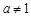 )的图象恒过定点,若点在一次函数
)的图象恒过定点,若点在一次函数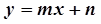 的图象上,其中
的图象上,其中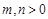 ,则
,则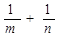 的最小值为( )
的最小值为( )| A.4 | B.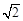 | C.2 | D.1 |
A
试题分析:根据指数函数的性质,可以求出A点,把A点代入一次函数y=mx+n,得出m+n=1,然后利用不等式的性质进行求解.
∵函数y=ax-1(a>0,且a≠1)的图象恒过定点A,可得A(1,1),∵点A在一次函数y=mx+n的图象上,∴m+n=1,∵m,n>0,∴m+n=1≥2
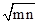 ,∴mn≤
,∴mn≤ ,所以
,所以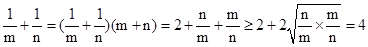 ,当且仅当n=m=1时取得等号。故选A.
,当且仅当n=m=1时取得等号。故选A.点评:解决该试题的关键找到指数函数必定过(0,1)点得到已知函数过点(1,1)

练习册系列答案
相关题目
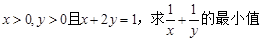 为_______________.
为_______________.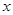 是实数,且满足等式
是实数,且满足等式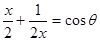 ,则实数
,则实数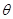 等于( )(以下各式中
等于( )(以下各式中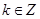 )
)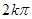
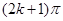
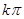
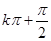
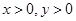 且
且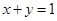 ,则
,则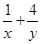 的最小值为______________。
的最小值为______________。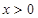 ,则
,则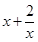 的最小值为 .
的最小值为 .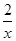 +
+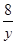 =1(x>0,y>0),则x+y的最小值为( )
=1(x>0,y>0),则x+y的最小值为( )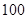 台洗衣机运往邻近的乡镇,现有
台洗衣机运往邻近的乡镇,现有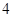 辆甲型货车和
辆甲型货车和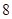 辆乙型货车可供使用.每辆甲型货车运输费用
辆乙型货车可供使用.每辆甲型货车运输费用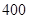 元,可装洗衣机
元,可装洗衣机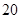 台;每辆乙型货车运输费用
台;每辆乙型货车运输费用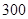 元,可装洗衣机
元,可装洗衣机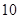 台.若每辆车至多只运一次,则该厂所花的最少运输费用为( )
台.若每辆车至多只运一次,则该厂所花的最少运输费用为( )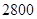 元
元 元
元 元
元 元
元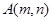 在直线
在直线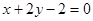 上,则
上,则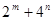 的最小值为
的最小值为 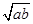
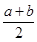 )2
)2