题目内容
已知平面向量a=(1,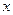 ),b=(2
),b=(2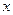 +3,-
+3,-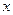 )(
)(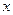 ∈R).
∈R).
(Ⅰ)若a⊥b,求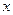 的值;
的值;
(Ⅱ)若a∥ b,求|a-b|.
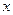 ),b=(2
),b=(2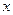 +3,-
+3,-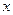 )(
)(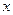 ∈R).
∈R).(Ⅰ)若a⊥b,求
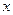 的值;
的值;(Ⅱ)若a∥ b,求|a-b|.
(Ⅰ) x=-1或x=3
(Ⅱ) 2
解:(Ⅰ)若a⊥b,则a·b=(1,x)·(2x+3,-x)=1×(2x+3)+x(-x)=0.
整理得:x2-2x-3=0,解得:x=-1或x=3. 4分
(Ⅱ)若a∥b,则有1×(-x)-x(2x+3)=0,即x(2x+4)=0.
解得:x=0或x=-2. 6分
当x=0时,a=(1,0),b=(3,0),
∴|a-b|=|(1,0)-(3,0)|=|(-2,0)|==2; 9分
当x=-2时,a=(1,-2),b=(-1,2),
∴|a-b|=|(1,-2)-(-1,2)|=|(2,-4)|==2. 12分
整理得:x2-2x-3=0,解得:x=-1或x=3. 4分
(Ⅱ)若a∥b,则有1×(-x)-x(2x+3)=0,即x(2x+4)=0.
解得:x=0或x=-2. 6分
当x=0时,a=(1,0),b=(3,0),
∴|a-b|=|(1,0)-(3,0)|=|(-2,0)|==2; 9分
当x=-2时,a=(1,-2),b=(-1,2),
∴|a-b|=|(1,-2)-(-1,2)|=|(2,-4)|==2. 12分

练习册系列答案
相关题目
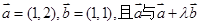 的夹角为锐角,则实数
的夹角为锐角,则实数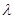 的取值范围是( )
的取值范围是( )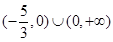
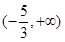
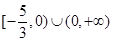
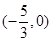
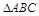 中,
中,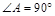 ,
,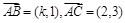 ,则k的值为()
,则k的值为()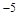
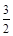
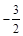
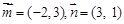 ,则向量
,则向量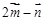 为
为 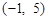
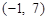
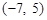
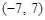
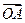 =(3,1),
=(3,1),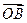 =(-1,2),向量
=(-1,2),向量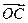 垂直于向量
垂直于向量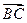 平行于
平行于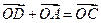 时,
时,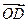 的坐标.
的坐标.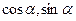 ),且0<
),且0<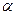 <
<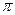 .
.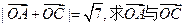 的夹角;
的夹角;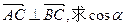 的值.
的值.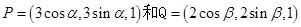 ,则|
,则|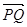 ︱的取值范围( )
︱的取值范围( )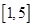
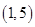
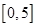
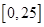
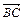 ="a,"
="a," 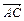 =b,则
=b,则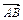 等于( )
等于( )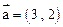 .
.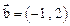 .
.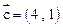
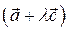 ∥
∥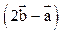 ,求实数
,求实数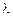 ;
;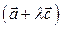 ⊥
⊥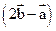 ,求实数
,求实数