题目内容
(本题满分12分)设数列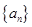 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且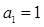 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)求数列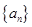 的通项公式;
的通项公式;
(Ⅲ)设数列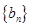 的前
的前 项和为
项和为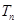 ,且
,且 ,证明:对一切正整数
,证明:对一切正整数 , 都有:
, 都有:
【答案】
(Ⅰ) ,
, ;(Ⅱ)
;(Ⅱ)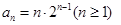
(Ⅲ)利用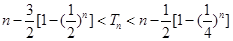 ,推出
,推出 。
。
【解析】
试题分析:(Ⅰ)∵
∴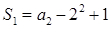


 …………………………………4分
…………………………………4分
(Ⅱ)由 得
得
检验知 ,
, 满足
满足
∴
变形可得
∴数列 是以1为首项,1为公差的等差
是以1为首项,1为公差的等差
解得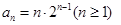 …………………………………………………7分
…………………………………………………7分
(Ⅲ)由(Ⅱ)知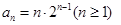
代入得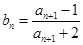 =
= ……………8分
……………8分
∵
∴
∴
∴
即
∴
 ∴
∴ …………………………………………………12分
…………………………………………………12分
考点:本题主要考查等差数列、等比数列的概念及其通项公式,数列的求和,不等式证明。
点评:典型题,本题首先由 的故选,确定数列的通项公式是关键。不等式证明中运用了“放缩法”,本题较难。
的故选,确定数列的通项公式是关键。不等式证明中运用了“放缩法”,本题较难。

练习册系列答案
相关题目
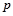 :实数
:实数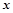 满足
满足 , 命题
, 命题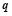 :实数
:实数 .
. 为真,求实数
为真,求实数 .
.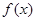 的单调区间;
的单调区间; 对
对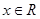 恒成立,求实数
恒成立,求实数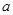 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式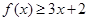 的解集;
的解集; 的解集为
的解集为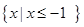 ,求a的值。
,求a的值。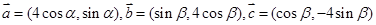
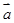 与
与 垂直,求
垂直,求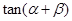 的值
的值  的最大值;
的最大值;  ,
,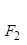 分别是椭圆
分别是椭圆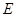 :
: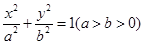 的左、右焦点,过
的左、右焦点,过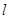 与
与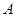 、
、 两点,且
两点,且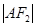 ,
,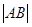 ,
,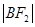 成等差数列,
成等差数列, 满足
满足 ,求
,求