Question

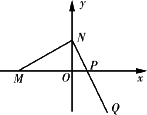
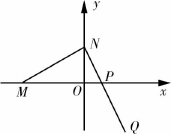
如图，已知M(-3m，0)(m＞0)，N、P两点分别在y轴和x轴上运动，并且满足，.

(Ⅰ)求动点Q的轨迹方程；

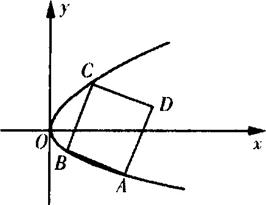
(Ⅱ)若正方形ABCD的三个顶点A、B、C在点Q的轨迹上，求正方形ABCD面积的最小值.

Answer 1

解：(1)设Q(x,y),因为,所以N(0,),

又M(-3m,0),所以=(3m,),=(x,),

由已知=0,则3mxy²=0,y²=4mx.

即Q点轨迹方程为y²=4mx.

(Ⅱ)如图,不妨设正方形在抛物线上的三个顶点中A、B在x轴的下方(包括x轴),记A、B、C的坐标分别为(x₁,y₁),(x₂,x₂),(x₃,y₃),其中y₃＞0≥y₂＞y₁并设直线AB的斜率为k(k＜0)

则有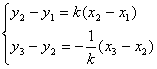                  ①

又因为A、B、C在抛物线y²=4mx上,故有x₁=,x₂=,x₃=代入①式得

y₁=y₂,y₃=-4mk-y₂                        ②

∵|AB|=|BC|即

∴(y₂-y₁)=(y₃-y₂)

∴(y₂-y₁)=-k(y₃-y₂)将②代入可得：y₂+y₂=-k(-4mk-2y₂)

即-4mk²-=-2(-k+1)y₂,得y₂=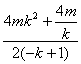

正方形的边长为|AB|=(y₃-y₂)=(-4mk-2y₂)

=(-4mk)=4m[-k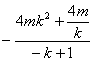-]=4m

易知所以4m

所以正方形ABCD面积的最小值为32m²