题目内容
在数列an中,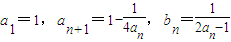 ,其中n∈N*.
,其中n∈N*.(1)求证:数列bn为等差数列;
(2)设
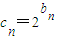 ,试问数列cn中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.
,试问数列cn中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.(3)已知当n∈N*且n≥6时,
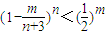 ,其中m=1,2,…n,求满足等式
,其中m=1,2,…n,求满足等式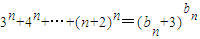 的所有n的值.
的所有n的值.
【答案】分析:(1)根据等差数列的性质,bn+1-bn为一个常数即可;
(2)设 ,试问数列cn中是否存在三项,它们可以构成等差数列,然后根据等差数列的性质,进行验证;
,试问数列cn中是否存在三项,它们可以构成等差数列,然后根据等差数列的性质,进行验证;
(3)已知当n∈N*且n≥6时,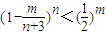 ,其中m=1,2,…n,等式
,其中m=1,2,…n,等式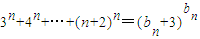 进行化简可化为3n+4n++(n+2)n=(n+3)n,然后进行放缩求解;
进行化简可化为3n+4n++(n+2)n=(n+3)n,然后进行放缩求解;
解答:解:(1)∵
∴数列bn为等差数列4;
(2)解:假设数列cn中存在三项,它们可以够成等差数列;不妨设为第p,r,q(p<r<q)项,
由(1)得bn=n,
∴cn=2n,
∴2•2r=2p+2q,
∴2r+1-p=1+2q-p
又2r+1-p为偶数,1+2q-p为奇数.
故不存在这样的三项,满足条件.
(3)由(2)得等式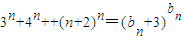
可化为3n+4n+…+(n+2)n=(n+3)n
即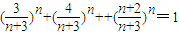
∴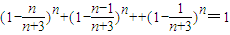
∵当n≥6时,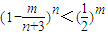 ,
,
∴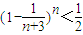 ,
,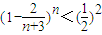 ,
,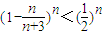 ,
,
∴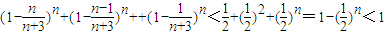
∴当n≥6时,3n+4n+…+(n+2)n<(n+3)n
当n=1,2,3,4,5时,
经验算n=2,3时等号成立
∴满足等式 的所有n=2,3;
的所有n=2,3;
点评:此题考等差数列的性质,前两问比较简单,第三问难度比较大,放缩时技巧性比较强,不等式与数列的综合题是高考的热点问题,也是压轴题;
(2)设
 ,试问数列cn中是否存在三项,它们可以构成等差数列,然后根据等差数列的性质,进行验证;
,试问数列cn中是否存在三项,它们可以构成等差数列,然后根据等差数列的性质,进行验证;(3)已知当n∈N*且n≥6时,
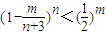 ,其中m=1,2,…n,等式
,其中m=1,2,…n,等式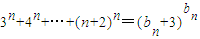 进行化简可化为3n+4n++(n+2)n=(n+3)n,然后进行放缩求解;
进行化简可化为3n+4n++(n+2)n=(n+3)n,然后进行放缩求解;解答:解:(1)∵

∴数列bn为等差数列4;
(2)解:假设数列cn中存在三项,它们可以够成等差数列;不妨设为第p,r,q(p<r<q)项,
由(1)得bn=n,
∴cn=2n,
∴2•2r=2p+2q,
∴2r+1-p=1+2q-p
又2r+1-p为偶数,1+2q-p为奇数.
故不存在这样的三项,满足条件.
(3)由(2)得等式
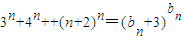
可化为3n+4n+…+(n+2)n=(n+3)n
即
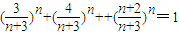
∴
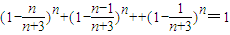
∵当n≥6时,
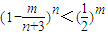 ,
,∴
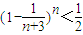 ,
,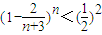 ,
,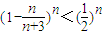 ,
,∴
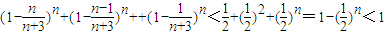
∴当n≥6时,3n+4n+…+(n+2)n<(n+3)n
当n=1,2,3,4,5时,
经验算n=2,3时等号成立
∴满足等式
 的所有n=2,3;
的所有n=2,3;点评:此题考等差数列的性质,前两问比较简单,第三问难度比较大,放缩时技巧性比较强,不等式与数列的综合题是高考的热点问题,也是压轴题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在数列{an}中,![]() ,其中θ为方程
,其中θ为方程![]() 的解,则这个数列的前n项和Sn为( )
的解,则这个数列的前n项和Sn为( )
|
| A. |
| B. |
| C. |
| D. |
|
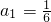 ,
,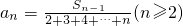 其中Sn表示数列的前n项和.
其中Sn表示数列的前n项和.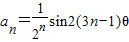 ,其中θ为方程
,其中θ为方程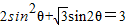 的解,则这个数列的前n项和Sn为( )
的解,则这个数列的前n项和Sn为( )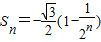
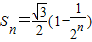
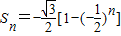
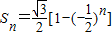
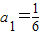 ,
,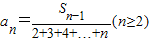 其中Sn表示数列的前n项和.
其中Sn表示数列的前n项和.