题目内容
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,M、N分别是
,M、N分别是![]() 和
和![]() 的中点.
的中点.
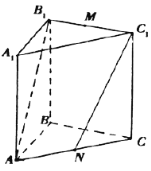
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)![]() (2)2
(2)2
【解析】
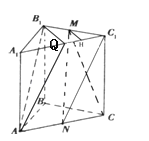
(1)过A作AQ∥C1N,交A1C1于Q,连接B1Q,可得∠B1AQ(或其补角)是异面直线AB1与C1N所成角.在△B1AQ中,分别求出AB1、AQ和B1Q的长,结合余弦定理算出cos∠B1AQ的值,从而得到异面直线AB1与C1N所成的角是arccos![]() ;
;
(2)平面A1B1C1中,过M作MH⊥A1C1于H.根据直三棱柱的性质结合面面垂直的性质定理,得到MH⊥平面AA1C1C,MH是三棱锥M﹣C1CN的高.算出MH的长和△C1CN的面积,结合三棱锥的体积公式,可得三棱锥M﹣C1CN的体积.
(1)平面AA1C1C中,过A作AQ∥C1N,交A1C1于Q,连接B1Q
∴∠B1AQ(或其补角)就是异面直线AB1与C1N所成的角
矩形AA1C1C中,N是AC中点,可得Q是A1C1中点
Rt△AA1B1中,AB1![]() 5,同理可得AQ
5,同理可得AQ![]()
∵等腰Rt△A1B1C1中,B1Q是斜边的中线
∴B1Q![]() A1B1=2
A1B1=2![]() ,
,
△B1AQ中,cos∠B1AQ![]() 0
0
∴∠B1AQ=arccos![]() ,即异面直线AB1与C1N所成的角等于arccos
,即异面直线AB1与C1N所成的角等于arccos![]() ;
;
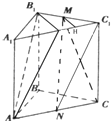
(2)平面A1B1C1中,过M作MH⊥A1C1于H
∵直三棱柱ABC﹣A1B1C1中,CC1⊥平面A1B1C1,CC1平面AA1C1C
∴平面AA1C1C⊥平面A1B1C1,
∵平面AA1C1C⊥平面A1B1C1=A1C1,MH⊥A1C1,
∴MH⊥平面AA1C1C,MH是三棱锥M﹣C1CN的高线
∵△B1C1Q中,M是B1C1中点,MH∥B1Q
∴MH是△B1C1Q的中位线,得MH![]()
∵△C1CN的面积S![]() CN×C1C
CN×C1C![]() 2
2![]() 3=3
3=3![]()
∴三棱锥M﹣C1CN的体积![]()
![]() 3
3![]() 2
2

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
选择全文 | 不选择全文 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
附: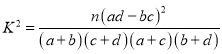 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
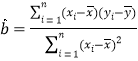
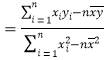 ,
,![]() .
.