题目内容
8.已知tan(π-α)=-$\frac{1}{2}$,求$\frac{2sin(π-α)-3cos(π+α)}{3cos(π-α)+4cos(\frac{π}{2}+α)}$.分析 直接利用诱导公式化简已知条件与所求的表达式然后求解即可.
解答 解:tan(π-α)=-$\frac{1}{2}$,可得tanα=$\frac{1}{2}$
$\frac{2sin(π-α)-3cos(π+α)}{3cos(π-α)+4cos(\frac{π}{2}+α)}$=$\frac{2sinα+3cosα}{-3cosα-4sinα}$=$\frac{2tanα+3}{-3-4tanα}$=$\frac{2×\frac{1}{2}+3}{-3-4×\frac{1}{2}}$=$-\frac{4}{5}$.
点评 本题考查诱导公式的应用,三角函数的化简求值,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知向量$\overrightarrow{a}$=(2,3),则与$\overrightarrow{a}$垂直的一个向量$\overrightarrow{b}$及$\overrightarrow{a}$的长度分别为( )
| A. | $\overrightarrow{b}$=(3,2),|$\overrightarrow{a}$|=5 | B. | $\overrightarrow{b}$=(-3,2),|$\overrightarrow{a}$|=13 | C. | $\overrightarrow{b}$=(3,-2),|$\overrightarrow{a}$|=5 | D. | $\overrightarrow{b}$=(3,-2),|$\overrightarrow{a}$|=$\sqrt{13}$ |
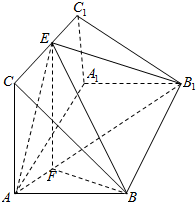 如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )
如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )