Question

（本小题满分12分）已知函数 ，且函数与的图像关于直线对称，又 ， .

（Ⅰ） 求的值域;

（Ⅱ） 是否存在实数m，使得命题   和   满足复合命题  为真命题？若存在，求出m的取值范围；若不存在，说明理由.

 

Answer 1

【答案】

（Ⅰ）的值域为

（Ⅱ）存在实数m，使得命题  为真命题，且m的取值范围为.

【解析】解：（Ⅰ）依题意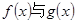互为反函数，由得

  ，得

     ……………………3分

故在上是减函数

  即 的值域为 . …………6分

（Ⅱ）由（Ⅰ）知是 上的减函数，是上的减函数，

又     …………9分

故     解得

因此，存在实数m，使得命题  为真命题，且m的取值范围为. ……………………12分