Question

（2013•山东）在平面直角坐标系xOy中，M为不等式组

2x+3y-6≤0 x+y-2≥0 y≥0

所表示的区域上一动点，则直线|OM|的最小值为

2

．

Answer 1

分析：首先根据题意做出可行域，欲求|OM|的最小值，由其几何意义为点O（0，0）到直线x+y-2=0距离为所求，代入点到直线的距离公式计算可得答案．

解答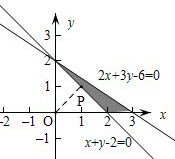：解：如图可行域为阴影部分，
由其几何意义为点O（0，0）到直线x+y-2=0距离，即为所求，
由点到直线的距离公式得：
d=

2

2

=

2

，
则|OM|的最小值等于

2

．
故答案为：

2

．

点评：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．