题目内容
15.曲线C1:ρsin(θ-$\frac{5π}{6}$)=1与C2:ρ=2$\sqrt{2}$cos(θ+$\frac{π}{4}$)的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 内含 |
分析 把极坐标方程分别化为直角坐标方程,求出圆心到直线的距离与半径比较即可得出.
解答 解:曲线C1:ρsin(θ-$\frac{5π}{6}$)=1展开为$-\frac{\sqrt{3}}{2}ρsinθ-\frac{1}{2}ρcosθ$=1,化为$x+\sqrt{3}y+2$=0,
C2:ρ=2$\sqrt{2}$cos(θ+$\frac{π}{4}$)展开为:${ρ}^{2}=2\sqrt{2}×\frac{\sqrt{2}}{2}$(ρcosθ-ρsinθ),化为x2+y2=2x-2y,平方为(x-1)2+(y+1)2=2,
∴圆心(1,-1)到直线的距离d=$\frac{|1-\sqrt{3}+2|}{2}$=$\frac{3-\sqrt{2}}{2}$,
∴d-r=$\frac{3-\sqrt{2}}{2}$-$\sqrt{2}$<0,
因此位置关系是相交.
故选:C.
点评 本题考查了把极坐标方程化为直角坐标方程、点到直线的距离公式、直线与圆的位置关系判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.某餐厅的原料费支出x与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为$\widehat{y}$=8.5x+7.5,则表中的m的值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 25 | 35 | m | 55 | 75 |
| A. | 50 | B. | 55 | C. | 60 | D. | 65 |
10.在平面直角坐标系中,若P(x,y)满足$\left\{\begin{array}{l}{x-4y+4≤0}\\{2x+y-10≤0}\\{5x-2y+2≥0}\end{array}\right.$,则当xy取得最大值时,点P的坐标为( )
| A. | (4,2) | B. | (2,2) | C. | (2,6) | D. | ($\frac{5}{2}$,5) |
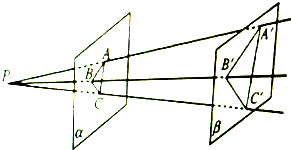 如图,从平面ABC外一点P,引射线PA、PB、PC,在它们上面分别取点A′、B′、C′,使$\frac{PA}{PA′}$=$\frac{PB}{PB′}$=$\frac{PC}{PC′}$,求证:平面ABC∥平面A′B′C′.
如图,从平面ABC外一点P,引射线PA、PB、PC,在它们上面分别取点A′、B′、C′,使$\frac{PA}{PA′}$=$\frac{PB}{PB′}$=$\frac{PC}{PC′}$,求证:平面ABC∥平面A′B′C′.