题目内容
已知两曲线参数方程分别为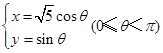 和
和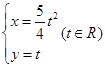 ,它们的交点坐标为 .
,它们的交点坐标为 .
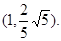
解析试题分析:因为,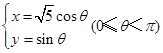 和
和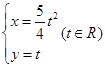
所以,有 ,
, ,解得,
,解得,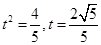 ,故交点坐标为
,故交点坐标为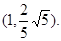
考点:极坐标方程、参数方程与直角坐标方程的互化,
点评:简单题,利用极坐标、直角坐标转化公式。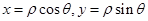 。参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。
。参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。

练习册系列答案
相关题目
方程
 为参数)所表示的曲线是( )
为参数)所表示的曲线是( )
| A.圆 | B.抛物线 | C.直线 | D.抛物线的一部分 |
题目内容
已知两曲线参数方程分别为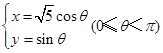 和
和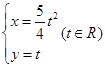 ,它们的交点坐标为 .
,它们的交点坐标为 .
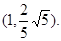
解析试题分析:因为,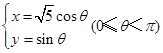 和
和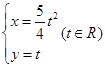
所以,有 ,
, ,解得,
,解得,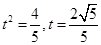 ,故交点坐标为
,故交点坐标为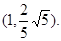
考点:极坐标方程、参数方程与直角坐标方程的互化,
点评:简单题,利用极坐标、直角坐标转化公式。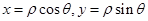 。参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。
。参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。

方程
 为参数)所表示的曲线是( )
为参数)所表示的曲线是( )
| A.圆 | B.抛物线 | C.直线 | D.抛物线的一部分 |