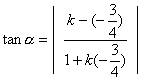题目内容
已知直线l过点P(2，3)，且和两条平行直线l1：3x+4y-7=0，l2：3x+4y+8=0分别相交于A、B两点，若|AB|=
，求直线l的方程．
答案：
解析：
解析：
要求出直线l的方程，已知直线l过定点P，故只需求出直线l的斜率即可，又由直线l与已知两平行直线相交而得到的线段长知道，故需先求出两条平行直线之间的距离，再看所求直线与已知直线所成的夹角多大，就可以求出直线l的斜率． 显然l与x轴垂直时，不满足条件． ∴ 可设直线l的方程为y-3=k(x-2)． 又l1与l2之间的距离为 设l与两条平行线的夹角为a ． 则由|AB｜= 又∵ 两平行线的斜率为- 由夹角公式可得： 解之得： ∴ 直线l的方程为y-3= 即x-7y+19=0或7x+y-17=0．
|
．
，
=3得a=45°．
，
或k=-7．
(x-2)或y-3=-7(x-2)．
练习册系列答案
相关题目
时，求直线l的方程．
x2+
x+3相切于P，若圆C满足下列两个条件：①与直线l切于点P；②与y轴相切，则圆C的方程为( )
)2+(y-5)2=
)2+(y-3)2=