Question

（2012•信阳模拟）若曲线C₁：x²+y²-2x=0与曲线C₂：y（y-mx-m）=0有四个不同的交点，则实数m的取值范围是

（-

3

3

，0）∪（0，

3

3

）

．

Answer 1

分析：把圆的方程化为标准方程，求出圆心和半径，直线过定点（-1，0），当直线y-mx-m=0与圆相切时，根据圆心到直线的距离d=

2m

m2+1

=r=1，求出m的值，数形结合求出实数m的取值范围．

解答：解：由题意可知曲线C₁：x²+y²-2x=0表示一个圆，化为标准方程得：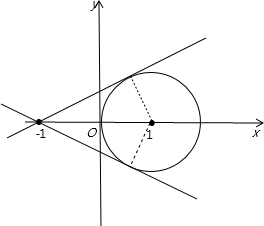
（x-1）²+y²=1，所以圆心坐标为（1，0），半径r=1；
C₂：y（y-mx-m）=0表示两条直线y=0和y-mx-m=0，
由直线y-mx-m=0可知：此直线过定点（-1，0），
在平面直角坐标系中画出图象如图所示：
当直线y-mx-m=0与圆相切时，圆心到直线的距离d=

2m

m2+1

=r=1，
化简得：m²=

1

3

，m=±

3

3

．
则直线y-mx-m=0与圆相交时，m∈（-

3

3

，0）∪（0，

3

3

），
故答案为 （-

3

3

，0）∪（0，

3

3

）．

点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，体现了数形结合的数学思想，属于中档题．