题目内容
已知函数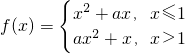 则“a≤-2”是“f(x)在R上单调递减”的
则“a≤-2”是“f(x)在R上单调递减”的
- A.充分而不必要条件
- B.必要而不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
C
分析:利用分段函数a的范围判断函数的单调性,利用函数的单调性求出a的范围,然后利用充要条件判断方法判断即可.
解答:函数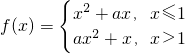 ,
,
当“a≤-2”时f(x)=x2+ax,x≤1是减函数,f(x)=ax2+x也是减函数,所以函数是单调减函数;
函数是减函数,则函数的对称轴满足: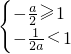 ?a≤2.
?a≤2.
所以函数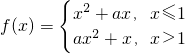 则“a≤-2”是“f(x)在R上单调递减”的充要条件.
则“a≤-2”是“f(x)在R上单调递减”的充要条件.
故选C.
点评:本题考查函数的单调性与函数的对称轴的应用,充要条件的判断.
分析:利用分段函数a的范围判断函数的单调性,利用函数的单调性求出a的范围,然后利用充要条件判断方法判断即可.
解答:函数
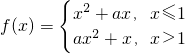 ,
,当“a≤-2”时f(x)=x2+ax,x≤1是减函数,f(x)=ax2+x也是减函数,所以函数是单调减函数;
函数是减函数,则函数的对称轴满足:
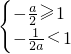 ?a≤2.
?a≤2.所以函数
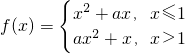 则“a≤-2”是“f(x)在R上单调递减”的充要条件.
则“a≤-2”是“f(x)在R上单调递减”的充要条件.故选C.
点评:本题考查函数的单调性与函数的对称轴的应用,充要条件的判断.

练习册系列答案
相关题目
 -2 (a>0且a≠1)的图像恒过定点A,则A的坐标为
-2 (a>0且a≠1)的图像恒过定点A,则A的坐标为 .
.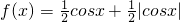 则
则 则“a≤-2”是“f(x)在R上单调递减”的( )
则“a≤-2”是“f(x)在R上单调递减”的( )