题目内容
已知“接龙等差”数列a1,a2,…,a10,a11,…,a20,a21,…,a30,a31,…构成如下:a1=1,a1,a2,…,a10是公差为1的等差数列;a10,a11,…,a20是公差为d的等差数列;a20,a21,…,a30是公差为d2的等差数列;…;a10n,a10n+1,a10n+2,…,a10n+10是公差为dn的等差数列(n∈N*);其中d≠0.(1)若a20=80,求d;
(2)设bn=a10n.求bn;
(3)当d>-1时,证明对所有奇数n总有bn>5.
【答案】分析:(1)由a1,a2,…,a10是首项为1,公差为1的等差数列得a10=10,由a10,a11,…,a20是公差为d的等差数列和a20=80,能求出d.
(2)由题意有a20=a10+10d,a30=a20+10d2,a40=a30+10d3,…a10n=a10(n-1)+10dn-1,由此能求出bn.
(3)设n为奇数,当d∈(0,+∞)时bn=10+10d+10d2+…+10dn-1>10,由此能求出当n为奇数且d>-1时,恒有bn>5.
解答:解:(1)由a1,a2,…,a10是首项为1,
公差为1的等差数列,得a10=10,
由a10,a11,…,a20是公差为d的等差数列,
得a20=a10+10d=10+10d=80,
解得d=7. …(4分)
(2)由题意有a20=a10+10d,
a30=a20+10d2,
a40=a30+10d3,
…
a10n=a10(n-1)+10dn-1
累加得a10n=a10+10d+10d2+…+10dn-1
=10+10d+10d2+…+10dn-1…(8分)
所以bn=10+10d+10d2+…+10dn-1
=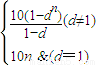 .…(10分)
.…(10分)
(3)设n为奇数,
当d∈(0,+∞)时,
bn=10+10d+10d2+…+10dn-1>10…(13分)
当d∈(-1,0)时,
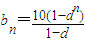 ,
,
由1<1-d<2及1-dn>1,
有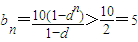
综上所述,当n为奇数且d>-1时,
恒有bn>5. …(16分)
点评:本题考查等差数列的公差的求法和通项公式的求法,考查运算能力和转化化归思想.解题时要认真申题,仔细解答,注意计算能力的培养.
(2)由题意有a20=a10+10d,a30=a20+10d2,a40=a30+10d3,…a10n=a10(n-1)+10dn-1,由此能求出bn.
(3)设n为奇数,当d∈(0,+∞)时bn=10+10d+10d2+…+10dn-1>10,由此能求出当n为奇数且d>-1时,恒有bn>5.
解答:解:(1)由a1,a2,…,a10是首项为1,
公差为1的等差数列,得a10=10,
由a10,a11,…,a20是公差为d的等差数列,
得a20=a10+10d=10+10d=80,
解得d=7. …(4分)
(2)由题意有a20=a10+10d,
a30=a20+10d2,
a40=a30+10d3,
…
a10n=a10(n-1)+10dn-1
累加得a10n=a10+10d+10d2+…+10dn-1
=10+10d+10d2+…+10dn-1…(8分)
所以bn=10+10d+10d2+…+10dn-1
=
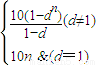 .…(10分)
.…(10分)(3)设n为奇数,
当d∈(0,+∞)时,
bn=10+10d+10d2+…+10dn-1>10…(13分)
当d∈(-1,0)时,
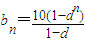 ,
,由1<1-d<2及1-dn>1,
有
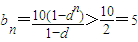
综上所述,当n为奇数且d>-1时,
恒有bn>5. …(16分)
点评:本题考查等差数列的公差的求法和通项公式的求法,考查运算能力和转化化归思想.解题时要认真申题,仔细解答,注意计算能力的培养.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目