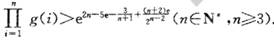题目内容
已知函数![]() (k为常数),
(k为常数),![]() 是函数
是函数![]() 图像上的点.
图像上的点.
(1)求实数k的值及函数![]() 的解析式;
的解析式;
(2)将![]() 的图像按向量
的图像按向量![]() 平移得到函数y=g(x)的图像.
平移得到函数y=g(x)的图像.
若![]() 对任意的
对任意的![]() 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.
(1)f-1(x)=log3(x+3),(x>-3) (2)![]()
解析:
(1)∵A(-2k, 2)是函数y=f-1(x)图像上的点.
∴B(2,-2K)是函数y=f(x)上的点. ∴-2k=32+k
∴k=-3, ∴y=f(x)=3x-3 ……………………………………………3分
∴y=f-1(x)=log3(x+3),(x>-3) …………………………6分
(2)将y=f-1(x)的图像按向量![]() =(3,0)平移,得函数y=g(x)=log3x(x>0) …………8分
=(3,0)平移,得函数y=g(x)=log3x(x>0) …………8分
要使2f-1(x+![]() )-g(x)≥1 恒成立,
)-g(x)≥1 恒成立,
即使2log3(x+![]() )-log3??x≥1恒成立.
)-log3??x≥1恒成立.
所以有x+![]() ≥3在x>0时恒成立,
≥3在x>0时恒成立,
只须(x+![]() )min≥3.……………………………………………………………11分
)min≥3.……………………………………………………………11分
又x+![]() (当且仅当x=
(当且仅当x=![]() 时取等号)
时取等号)
∴(x+![]() )min=4
)min=4![]() ,
,
只须4![]() ≥3,即m≥
≥3,即m≥![]() .
.
∴实数m的取值范围为![]() …………………………………………………………14分
…………………………………………………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
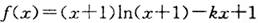 ,,k为常数,e是自然对数的底数).
,,k为常数,e是自然对数的底数).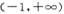 上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;
上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;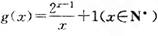 ,记
,记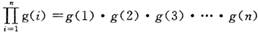 ,求证:
,求证: