题目内容
如果对于任意实数a,b(a<b),随机变量X满足P(a<X≤b)=
?μ,σ(x)dx,称随机变量X服从正态分布,记为N(μ,σ2),若X~(0,1),P(X>1)=p,则
?μ,σ(x)dx=
-p
-p.
| ∫ | b a |
| ∫ | 0 -1 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据所给的新定义的正态分布,写出要求的表示式所对应的意义,根据正弦曲线关于对称轴的对称性,得到要求的结果.
解答:解:∵P(a<X≤b)=
?μ,σ(x)dx,
∴∫0-1?μ,σ(x)dx=P(-1<X≤0)
∵若X~(0,1),P(X>1)=p
P(-1<X≤0)=
-p
故答案为
-p
| ∫ | b a |
∴∫0-1?μ,σ(x)dx=P(-1<X≤0)
∵若X~(0,1),P(X>1)=p
P(-1<X≤0)=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查正态分布曲线的特点及曲线所表示的意义,本题解题的关键是列举所给的新定义,并且能够简单的应用新定义.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
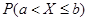 =
=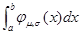 ,称随机变量X服从正态分布,记为
,称随机变量X服从正态分布,记为 ,若X~(0,1),P(X>1)=p,则
,若X~(0,1),P(X>1)=p,则 =________
=________ =
= ,称随机变量X服从正态分布,记为
,称随机变量X服从正态分布,记为 ,若X~(0,1),P(X>1)=p,则
,若X~(0,1),P(X>1)=p,则 =_________
=_________ ,称随机变量X服从正态分布,记为N(μ,σ2),若X~(0,1),P(X>1)=p,则
,称随机变量X服从正态分布,记为N(μ,σ2),若X~(0,1),P(X>1)=p,则 = .
= .