题目内容
给出下列四个结论:
(1) 设A、B是两个非空集合,如果按对应法则f,使对于集合A中的任意一个元素x,在集合B中都有元素y与之对应,则称对应f:A→B为从A到B的映射;
(2) 函数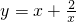 在区间[2,+∞)上单调递增;
在区间[2,+∞)上单调递增;
(3) 若a,b是异面直线,a?平面α,b?平面β,则α∥β;
(4) 两条直线有斜率,如果它们的斜率相等,则它们平行.则其中所有正确结论的序号是 ________.
解:(1) 设A、B是两个非空集合,如果按对应法则f,使对于集合A中的任意一个元素x,在集合B中都有唯一元素y与之对应,则称对应f:A→B为从A到B的映射,缺少关键词“唯一”,故不正确;
(2) 函数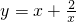 在区间[
在区间[ ,+∞)上单调递增,则在区间[2,+∞)上单调递增,故正确;
,+∞)上单调递增,则在区间[2,+∞)上单调递增,故正确;
(3) 若a,b是异面直线,a?平面α,b?平面β,则α∥β或α与β相交,故不正确;
(4) 两条直线有斜率,如果它们的斜率相等,则它们平行或重合,故不正确.
故答案为:(2)
分析:对于(1)根据映射的定义进行判定,对于(2)根据对勾函数的单调性进行判定,对于(3)根据线面关系进行判定,对于(4)注意直线重合的情况.
点评:本题主要考查了映射的定义,以及函数的单调性和线面位置关系、斜率等有关问题,属于基础题.
(2) 函数
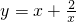 在区间[
在区间[ ,+∞)上单调递增,则在区间[2,+∞)上单调递增,故正确;
,+∞)上单调递增,则在区间[2,+∞)上单调递增,故正确;(3) 若a,b是异面直线,a?平面α,b?平面β,则α∥β或α与β相交,故不正确;
(4) 两条直线有斜率,如果它们的斜率相等,则它们平行或重合,故不正确.
故答案为:(2)
分析:对于(1)根据映射的定义进行判定,对于(2)根据对勾函数的单调性进行判定,对于(3)根据线面关系进行判定,对于(4)注意直线重合的情况.
点评:本题主要考查了映射的定义,以及函数的单调性和线面位置关系、斜率等有关问题,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=