题目内容
【题目】已知命题p：“曲线C1：
=1表示焦点在x轴上的椭圆”，命题q：“曲线C2：
表示双曲线”．
（1）若命题p是真命题，求m的取值范围；
（2）若p是q的必要不充分条件，求t的取值范围．
【答案】（1）-4＜m＜-2，或m＞4；（2）-4≤t≤-3或t≥4
【解析】
（1）方程表示焦点在
轴上的椭圆需满足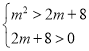
，解不等式即可求解（2）化简命题q可得t＜m＜t+1，利用p是q的必要不充分条件可知{m|t＜m＜t+1}
{m|-4＜m＜-2，或m＞4}，建立不等式求解即可.
（1）若p为真：则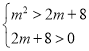，解得-4＜m＜-2，或m＞4；
（2）若q为真，则（m-t)(m-t-1)＜0，即t＜m＜t+1，∵p是q的必要不充分条件，
则{m|t＜m＜t+1}{m|-4＜m＜-2，或m＞4}，
即
或t≥4，解得-4≤t≤-3或t≥4.
练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组 | 频数 | 频率 |
[10，15） | 10 | 0.25 |
[15，20） | 25 | n |
[20，25） | m | p |
[25，30） | 2 | 0.05 |
合计 | M | 1 |
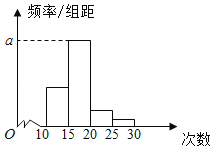
（1）求出表中M，p及图中a的值；
（2）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，请列举出所有基本事件，并求至多1人参加社区服务次数在区间[20，25）内的概率．
