若抛物线y=2x2上的两点A(x1,y1).B(x2,y2)关于直线l:y=x+m对称,且x1x2=-,求实数m的值. 题目和参考答案——青夏教育精英家教网——

题目内容

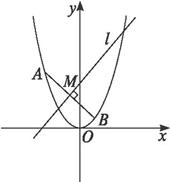
若抛物线y=2x²上的两点A(x₁,y₁)、B(x₂,y₂)关于直线l:y=x+m对称,且x₁x₂=-,求实数m的值.

试题答案

相关练习册答案

思路解析：关于直线对称,则满足①与直线垂直，②中点在直线上.

解：如图所示，∵A、B两点关于直线l对称，

∴AB⊥l且AB中点M（x₀，y₀）在直线l上.

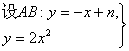
2x²+x-n=0,

∴x₁+x₂=-,x₁x₂=-.

由x₁x₂=-得n=1,

又x₀==-,y₀=-x₀+n=+1=,

即点M为(-,),由点M在直线l上,得=-+m.

∴m=.

练习册系列答案

芝麻开花暑假作业江西教育出版社系列答案

非常假期集结号暑假安徽文艺出版社系列答案

永乾图书快乐假期暑假作业延边人民出版社系列答案

文诺文化快乐假期暑假作业延边人民出版社系列答案

暑假作业新疆青少年出版社系列答案

暑假作业吉林人民出版社系列答案

津桥教育暑假提优衔接新世界出版社系列答案

暑假作业假期园地中原农民出版社系列答案

系统集成暑假生活北京师范大学出版社系列答案

快乐暑假假期面对面南方出版社系列答案

相关题目

若抛物线y=2x²上的两点A（x₁，y₁）、B（x₂，y₂）关于直线y=x+m对称且x₁x₂=-

，求m的值．

若抛物线y=2x²上的两点A(x₁,y₁),B(x₂,y₂)关于直线y=x+m对称,且x₁x₂=-,求m的值.

若抛物线y=2x²上两点A(x₁,y₁)、B(x₂,y₂)关于直线y=x+m对称,且x₁x₂=-,则实数m的值为________________.

若抛物线y=2x²上两点A(x₁,y₁)、B(x₂,y₂)关于直线y=x+M对称,且x₁·x₂=,则M等于(　　)

A. B. C.-3 D.3