题目内容
已知点A(0,2)、B(1,-1)、C(2,-4),求证:A、B、C三点共线.
证明见解析
证明:∵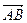 =(1-0,-1-2)=(1,-3).
=(1-0,-1-2)=(1,-3).
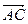 =(2-0,-4-2)=(2,-6)
=(2-0,-4-2)=(2,-6)
又1×(-6)-2×(-3)=0,∴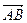 ∥
∥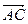
又直线AB、直线AC有公共点A
∴A、B、C三点共线.
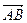 =(1-0,-1-2)=(1,-3).
=(1-0,-1-2)=(1,-3).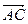 =(2-0,-4-2)=(2,-6)
=(2-0,-4-2)=(2,-6)又1×(-6)-2×(-3)=0,∴
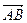 ∥
∥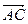
又直线AB、直线AC有公共点A
∴A、B、C三点共线.

练习册系列答案
相关题目
 是
是 的三条高,求证:
的三条高,求证:
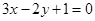 所对应的直线经过伸缩变换
所对应的直线经过伸缩变换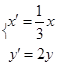 后的直线方程。
后的直线方程。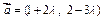 与
与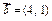 共线,则
共线,则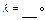
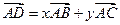 ,则
,则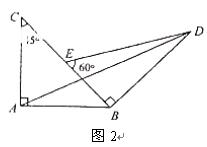
 是不共线的任意三点,则以下各式中成立的是( )
是不共线的任意三点,则以下各式中成立的是( )



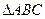 的内角,
的内角,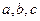 分别是其对边长,向量
分别是其对边长,向量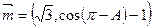 ,
,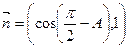 ,
,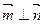 .求角A的大小;
.求角A的大小;