题目内容
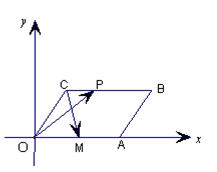
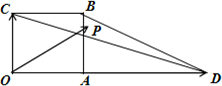
已知四边形OABC是边长为1的正方形,
=3
,点P为△BCD内(含边界)的动点,设
=α
+β
(α、β∈R),则α+β的最大值等于
.
| OD |
| OA |
| OP |
| OC |
| OD |
| 4 |
| 3 |
| 4 |
| 3 |
分析:先建立以O为原点,以OD所在直线为x轴的直角坐标系,根据条件求出点P的坐标与α,β之间的关系,再根据点P的位置,
借助于可行域即可求解.
借助于可行域即可求解.
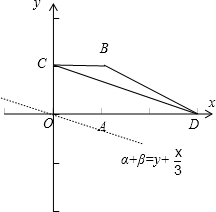
解答:解:以O为原点,以OD所在直线为x轴建立直角坐标系,
设点P(x,y),则(x,y)=α(0,1)+β(3,0)=(3β,α),
所以 x=3β,y=α,α+β=y+
.
由于点P在△BCD内(包含边界),目标函数为α+β=y+
,如图(2)所示,
当点P为点B(1,1)时,α+β=y+
取得最大值,其最大值为1+
=
,
故答案为:
.
(2)(1)
设点P(x,y),则(x,y)=α(0,1)+β(3,0)=(3β,α),
所以 x=3β,y=α,α+β=y+
| x |
| 3 |
由于点P在△BCD内(包含边界),目标函数为α+β=y+
| x |
| 3 |
当点P为点B(1,1)时,α+β=y+
| x |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |


(2)(1)
点评:本题主要考查相等向量以及线性规划的简单应用,是对知识点的综合考查,考查计算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 在平面直角坐标系xOy中,已知四边形OABC是平行四边形,且点
在平面直角坐标系xOy中,已知四边形OABC是平行四边形,且点 在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,
在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,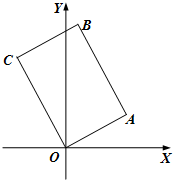 如图,已知四边形OABC是矩形,O是坐标原点,O、A、B、C按逆时针排列,A的坐标是
如图,已知四边形OABC是矩形,O是坐标原点,O、A、B、C按逆时针排列,A的坐标是 分)
分)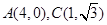 ,点M是OA的中点,点P在线段BC上运动(包括端点),如图
,点M是OA的中点,点P在线段BC上运动(包括端点),如图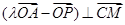 ?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。
?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。