题目内容
(1)已知A={2,3},B={x|x2+ax+b=0},A∩B={2},A∪B=A,求a+b的值;
(2)计算lg20+log10025+2
×
×
.
(2)计算lg20+log10025+2
| 3 |
| 6 | 12 |
| 3 | 1.5 |
(1)∵A∩B={2},∴2∈B
而A∪B=A,A={2,3},
∴B⊆A
∴B={2}或{2,3},
当B={2}时,2是x2+ax+b=0是方程两个相等的实根,2+2=-a=-4,解得:a=4
2×2=b=4,
∴a+b=0
当B={2,3}时,2,3是x2+ax+b=0是方程两个实根,2+3=-a=5,解得:a=-5
2×3=b=6,
∴a+b=1
∴a+b=0或1
(2)lg20+log10025+2
×
×
=lg10×2+
+2×3
×12
×(
)
=1+lg2+lg5+6=8
而A∪B=A,A={2,3},
∴B⊆A
∴B={2}或{2,3},
当B={2}时,2是x2+ax+b=0是方程两个相等的实根,2+2=-a=-4,解得:a=4
2×2=b=4,
∴a+b=0
当B={2,3}时,2,3是x2+ax+b=0是方程两个实根,2+3=-a=5,解得:a=-5
2×3=b=6,
∴a+b=1
∴a+b=0或1
(2)lg20+log10025+2
| 3 |
| 6 | 12 |
| 3 | 1.5 |
| lg25 |
| lg100 |
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的定义域为M,g(x)=
的定义域为M,g(x)= 的定义域为N,则M∩N=
的定义域为N,则M∩N= 
 ,则
,则 ( )
( )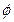

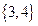

 } ,若A
} ,若A  B ="{" 0, 1, 2, 4 ,16},则
B ="{" 0, 1, 2, 4 ,16},则 的值为( )A 0 B 1 C 2 D 4
的值为( )A 0 B 1 C 2 D 4