Question

抛物线y²=4x的焦点为F，点A，B在抛物线上，且∠AFB=

2π

3

，弦AB中点M在准线l上的射影为M′，则

|MM′|

|AB|

的最大值为（　　）

• A．

  4 3

  3

• B．

  3

• C．

  2 3

  3

• D．

  3

  3

Answer 1

分析：设AF=a，BF=b，由抛物线定义得2|MM′|=a+b．再由余弦定理得|AB|²=a²+b²-2abcos

2π

3

，结合不等式a+b≥2

ab

求得|AB|的范围，把|MM′|和|AB|作比可得答案．

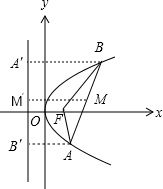解答：解：如图，
设AF=a（a＞0），BF=b（b＞0），由抛物线定义，得2|MM′|=a+b．
在△ABF中，由余弦定理，得|AB|²=a²+b²-2abcos

2π

3

=a²+b²+ab=（a+b）²-ab，
∵a＞0，b＞0，由基本不等式得：a+b≥2

ab

，∴ab≤

(a+b)2

4

，
∴(a+b)2-ab≥

3

4

(a+b)2．
即|AB|2≥

3

4

(a+b)2，∴|AB|≥

3

2

(a+b)．
∴

|MM′|

|AB|

≤

a+b 2

3 2 (a+b)

=

3

3

．
∴

|MM′|

|AB|

的最大值为

3

3

．
故选：D．

点评：本题主要考查对抛物线定义的应用和余弦定理的应用．训练了基本不等式的用法，考查了学生综合分析问题和解决问题的能力，是中档题．