题目内容
设{an}(n∈N*)是等差数列,Sn是其前n项的和,且S5<S6,S6=S7>S8,则下列结论错误的是( )
| A.d<0 | B.a7=0 |
| C.S9>S5 | D.S6与S7均为Sn的最大值 |
C
解析试题分析:根据题设条件且S5<S6,S6=S7>S8,则可判断A的正确性;∵且S5<S6,S6=S7>S8,则a7=0,可判断B正确;∵在等差数列中Sn等差数列的前n项和公式存在最大值可判断数列的单调性,这样可判断D的正确性;利用数列的前n项和定义与等差数列的性质,来判断D的正确性解:∵S5<S6,S6=S7>S8,则A正确;∵S6=S7,∴a7=0,∴B正确;∵S5<S6,S6=S7>S8,则a6>0,a7=0,a8<0,∴d<0,A正确∵a6+a7+a8+a9=2(a7+a8)<0,∴S9<S5,C错误.故选C
考点:命题的真假, 等差数列的前n项和公式
点评:本题借助考查命题的真假判断,考查等差数列的前n项和公式及等差数列的性质.在等差数列中Sn存在最大值的条件是:a1>0,d<0.一般两种解决问题的思路:项分析法与和分析法

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
下列说法中正确的是( )
| A.一个命题的逆命题为真,则它的逆否命题一定为真 |
B.“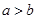 ”与“ ”与“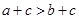 ”不等价 ”不等价 |
C.“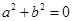 ,则 ,则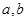 全为 全为 ”的逆否命题是“若 ”的逆否命题是“若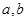 全不为 全不为 , 则 , 则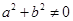 ” ” |
| D.一个命题的否命题为真,则它的逆命题一定为真 |
下列说法中,正确的是
A.命题“若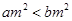 ,则 ,则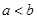 ”的逆命题是真命题; ”的逆命题是真命题; |
B.命题“ , ,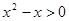 ”的否定是:“ ”的否定是:“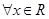 , ,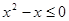 ”; ”; |
C.命题“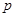 或 或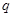 ”为真命题,则命题“ ”为真命题,则命题“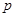 ”和命题“ ”和命题“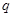 ”均为真命题; ”均为真命题; |
D.已知 ,则“ ,则“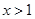 ”是“ ”是“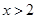 ”的充分不必要条件. ”的充分不必要条件. |
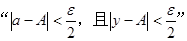 是
是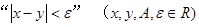 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题p: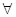 x1,x2
x1,x2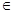 R,(f(x2)
R,(f(x2) f(x1))(x2
f(x1))(x2 x1)≥0,则
x1)≥0,则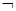 p是
p是
A.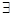 x1,x2 x1,x2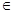 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)≤0 x1)≤0 |
B.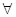 x1,x2 x1,x2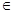 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)≤0 x1)≤0 |
C.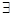 x1,x2 x1,x2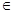 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)<0 x1)<0 |
D.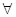 x1,x2 x1,x2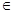 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)<0 x1)<0 |
设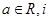 是虚数单位,则“
是虚数单位,则“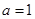 ”是“
”是“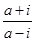 为纯虚数”的( )
为纯虚数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
“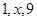 成等比数列”是“
成等比数列”是“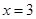 ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“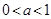 ”是“
”是“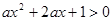 的解集是实数集
的解集是实数集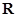 ”的( )
”的( )
| A.充分而非必要条件 | B.必要而非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
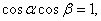 则
则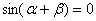 ;②已知直线
;②已知直线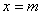 与函数
与函数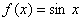 ,
,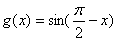 的图象分别交于
的图象分别交于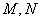 两点,则
两点,则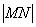 的最大值为
的最大值为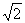 ;
;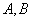 是△
是△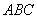 的两内角,如果
的两内角,如果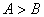 ,则
,则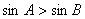 ;
;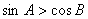 。
。