题目内容
(本小题满分12分)定义在 上的函数
上的函数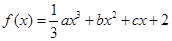 同时满足以下条件:
同时满足以下条件:
① 在
在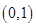 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
②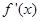 是偶函数;
是偶函数;
③ 在
在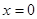 处的切线与直线
处的切线与直线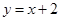 垂直.
垂直.
(1)求函数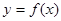 的解析式;
的解析式;
(2)设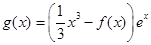 ,求函数
,求函数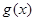 在
在 上的最小值.
上的最小值.
【答案】
(1)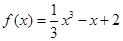 . (2)
. (2)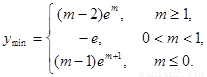 。
。
【解析】本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,解题的关键是确定函数的单调性
(1)求导函数,可得f′(x)=ax2+2bx+c,根据R上的函数f(x)= 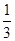 ax3+bx2+cx+2同时满足的条件,列出方程组,从而可求函数y=f(x)的解析式;
ax3+bx2+cx+2同时满足的条件,列出方程组,从而可求函数y=f(x)的解析式;
(2)求导函数,确定函数的单调性,再结合区间,进行分类讨论,即可求得g(x)在[m,m+1]上的最小值.
解:(1)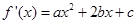 .
.
由题意知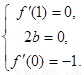 即
即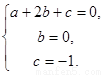 解得
解得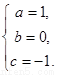
所以函数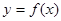 的解析式为
的解析式为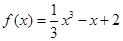 . . …………….…….……4分
. . …………….…….……4分
(2)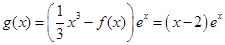 ,
, 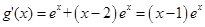 .
.
令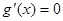 得
得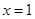 ,所以函数
,所以函数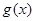 在
在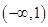 递减,在
递减,在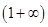 递增. ……6分
递增. ……6分
当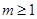 时,
时,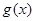 在
在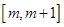 单调递增,
单调递增,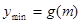
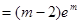 .
.
当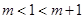 时,即
时,即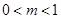 时,
时,
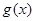 在
在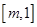 单调递减,在
单调递减,在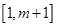 单调递增,
单调递增,
 . ……9分
. ……9分
当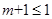 时,即
时,即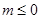 时,
时,
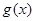 在
在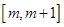 单调递减,
单调递减,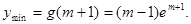
综上,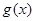 在
在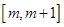 上的最小值
上的最小值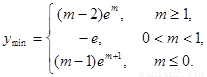 ……12分
……12分

练习册系列答案
相关题目