题目内容
(本小题满分12分)
某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第一组 [160,164],第二组[164,168],…,第6组[180,184],下图是按上述分组方法得到的频率分布直方图.

(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172 cm以上(含172 cm)的人数;
(Ⅲ)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为 ,求
,求 的数学期望.
的数学期望.
参考数据:
若 .则
.则
 =0.6826,
=0.6826,
 ="0.9544,"
="0.9544,"
 =0.9974.
=0.9974.
(Ⅰ)高于全市的平均值168。
(Ⅱ)这50名男生身高在172 cm以上(含172 cm)的人数为10人.
(Ⅲ)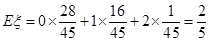
【解析】
试题分析:(Ⅰ)由直方图,经过计算该校高三年级男生平均身高为
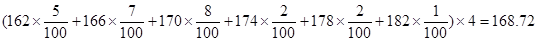 ,
,
高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168). …………………………………………………………(4分)
(Ⅱ)由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×5=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10人. ……………(6分)
(Ⅲ)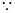
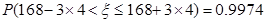 ,
,
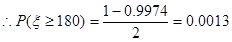 ,0.0013×100 000=130.
,0.0013×100 000=130.
所以,全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量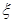 可取
可取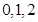 ,于是
,于是
 ,
,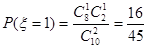 ,
,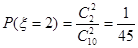
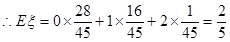 .
…………………(12分)
.
…………………(12分)
考点:本题主要考查离散性随机变量的分布列及数学期望。
点评:本题是对频率、频数灵活运用的综合考查,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率= .涉及组合数计算要细心。
.涉及组合数计算要细心。

 阅读快车系列答案
阅读快车系列答案