题目内容
设M是由满足下列两个条件的函数f(x)构成的集合:(1)方程f(x)-1=0有实数解;
(2)函数f(x)的导数f'(x)满足0<f'(x)<2,给出如下函数:
①f(x)=x+sinx;
②
 ;
;③f(x)=x+log3x,x∈[1,+∞);
④f(x)=x+2x.
其中是集合M中的元素的有 .(只需填写函数的序号)
【答案】分析:条件(1)可以利用函数的零点判断根的问题,条件(2)先求出每一个函数导数,后可以代入特殊值进行检验筛选.
解答:解:①∵f(x)=x+sinx,∴由f(x)-1=0,得x-1+sinx=0
分别做出函数y=x-1和y=sinx的图象知,二者有一个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵f'(x)=1-cosx,-1≤cosx≤1,
∴0≤f(x)≤2,即条件(2)不成立.
故①不是集合M中的元素.
②∵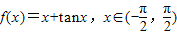 ,
,
∴由f(x)-1=0,得x+tanx-1=0,
分别做出函数y=x-1和y=tanx的图象知,二者有一个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵f'(x)=1+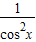 ,∴条件(2)不成立.
,∴条件(2)不成立.
故②不是集合M中的元素.
③∵f(x)=x+log3x,x∈[1,+∞),
∴由f(x)-1=0,得x+log3x-1=0,
分别做出函数y=x-1和y=log3x的图象知,二者有两个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵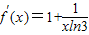 ,∴条件(2)成立.
,∴条件(2)成立.
故③是集合M中的元素.
④∵f(x)=x+2x.∴由f(x)-1=0,得x+2x-1=0,
分别做出函数y=x-1和y=2x的图象知,二者有一个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵f'(x)=1+2xln2,∴条件(2)不成立.
故④不是集合M中的元素.
故答案为③.
点评:本题考查导数的运算,解题时要认真审题,注意零点的运用.
解答:解:①∵f(x)=x+sinx,∴由f(x)-1=0,得x-1+sinx=0
分别做出函数y=x-1和y=sinx的图象知,二者有一个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵f'(x)=1-cosx,-1≤cosx≤1,
∴0≤f(x)≤2,即条件(2)不成立.
故①不是集合M中的元素.
②∵
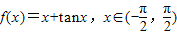 ,
,∴由f(x)-1=0,得x+tanx-1=0,
分别做出函数y=x-1和y=tanx的图象知,二者有一个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵f'(x)=1+
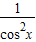 ,∴条件(2)不成立.
,∴条件(2)不成立.故②不是集合M中的元素.
③∵f(x)=x+log3x,x∈[1,+∞),
∴由f(x)-1=0,得x+log3x-1=0,
分别做出函数y=x-1和y=log3x的图象知,二者有两个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵
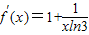 ,∴条件(2)成立.
,∴条件(2)成立.故③是集合M中的元素.
④∵f(x)=x+2x.∴由f(x)-1=0,得x+2x-1=0,
分别做出函数y=x-1和y=2x的图象知,二者有一个交点,
∴方程f(x)-1=0有实数解.即条件(1)成立.
∵f'(x)=1+2xln2,∴条件(2)不成立.
故④不是集合M中的元素.
故答案为③.
点评:本题考查导数的运算,解题时要认真审题,注意零点的运用.

练习册系列答案
相关题目
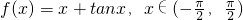 ;
;