Question

在数列{a_n}中，a₁＝1，当n≥2时，a_n，S_n，S_n－成等比数列.

(1)求a₂，a₃，a₄，并推出a_n的表达式；

(2)用数学归纳法证明所得的结论.

Answer 1

【解析】∵a_n，S_n，S_n－成等比数列，

∴＝a_n·(S_n－)(n≥2)　　　(*)

(1)由a₁＝1，得S₂＝a₁＋a₂＝1＋a₂，

代入(*)式得：a₂＝－，

由a₁＝1，a₂＝－，得

S₃＝＋a₃代入(*)式得：a₃＝－，

同理可得：a₄＝－，由此可推出：

a_n＝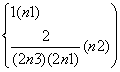

(2)①当n＝1,2,3,4时，由(1)知猜想成立.

②假设n＝k(k≥2)时，a_k＝－成立，

故＝－·(S_k－)

∴(2k－3)(2k－1)＋2S_k－1＝0

∴S_k＝，S_k＝－(舍)

由S_k＋1²＝a_k＋1·(S_k＋1－)，

得(S_k＋a_k＋1)²＝a_k＋1(a_k＋1＋S_k－)

⇒＋a_k＋1²＋＝a_k＋1²＋－a_k＋1

⇒a_k＋1＝，即n＝k＋1时命题也成立.

由①②知，a_n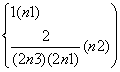＝对一切n∈N_＋成立.