题目内容
(2012•陕西)设函数fn(x)=xn+bx+c(n∈N+,b,c∈R)
(1)设n≥2,b=1,c=-1,证明:fn(x)在区间(
,1)内存在唯一的零点;
(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,求b的取值范围.
(1)设n≥2,b=1,c=-1,证明:fn(x)在区间(
| 1 | 2 |
(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,求b的取值范围.
分析:(1)当b=1,c=-1,n≥2时,f(x)=xn+x-1,易求f(
)f(1)<0,再用导数判断f(x)的单调性即可使结论得证;
(2)解法一,由题意知
,即
,作出图,用线性规划的知识即可使问题解决;
解法二,由-1≤f(1)=1+b+c≤1,即-2≤b+c≤0①,-1≤f(-1)=1-b+c≤1,即-2≤-b+c≤0②,由①②可求得:-6≤b+3c≤0,问题即可解决;
解法三 由题意知
,解得b=
,c=
,b+3c=2f(1)+f(-1)-3,由-6≤b+3c≤0,可得答案;
(3)当n=2时,f(x)=x2+bx+c,对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,等价于在[-1,1]上最大值与最小值之差M≤4,据此分类讨论解决即可.
| 1 |
| 2 |
(2)解法一,由题意知
|
|
解法二,由-1≤f(1)=1+b+c≤1,即-2≤b+c≤0①,-1≤f(-1)=1-b+c≤1,即-2≤-b+c≤0②,由①②可求得:-6≤b+3c≤0,问题即可解决;
解法三 由题意知
|
| f(1)-f(-1) |
| 2 |
| f(1)+f(-1)+2 |
| 2 |
(3)当n=2时,f(x)=x2+bx+c,对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,等价于在[-1,1]上最大值与最小值之差M≤4,据此分类讨论解决即可.
解答:解:(1)当b=1,c=-1,n≥2时,f(x)=xn+x-1
∵f(
)f(1)=(
-
)×1<0,∴f(x)在区间(
,1)内存在零点,
又当x∈(
,1)时,f′(x)=nxn-1+1>0,
∴f(x)在(
,1)上单调递增,∴f(x)在区间(
,1)内存在唯一的零点;
(2)解法一 由题意知
,即
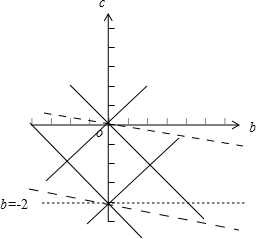
由图象知b+3c在点(0,-2)取到最小值-6,在点(0,0)处取到最大值0,
∴b+3c的最小值为-6,最大值为0;
解法二 由题意知
-1≤f(1)=1+b+c≤1,即-2≤b+c≤0,①
-1≤f(-1)=1-b+c≤1,即-2≤-b+c≤0,②
①×2+②得:-6≤2(b+c)+(-b+c)=b+3c≤0,
当b=0,c=-2时,b+3c=-6;当b=c=0,时,b+3c=0;
∴b+3c的最小值为-6,最大值为0;
解法三 由题意知
,解得b=
,c=
,
∴b+3c=2f(1)+f(-1)-3,
∵-1≤f(-1)≤1,-1≤f(1)≤1,
∴-6≤b+3c≤0,
当b=0,c=-2时,b+3c=-6;当b=c=0,时,b+3c=0;
∴b+3c的最小值为-6,最大值为0;
(3)当n=2时,f(x)=x2+bx+c,对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,等价于在[-1,1]上最大值与最小值之差M≤4,据此分类讨论如下:
(i)当|
|>1,即|b|>2,M=|f(1)-f(-1)|=2|b|>4,与题设矛盾;
(ii)当-1≤-
<0,即0<b≤2时,M=f(1)-f(-
)=(
+1)2≤4恒成立,
(iii)当0≤-
≤1,即-2≤b≤0时,M=f(-1)-f(-
)=(
-1)2≤4恒成立,
综上所述,-2≤b≤2.
∵f(
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
又当x∈(
| 1 |
| 2 |
∴f(x)在(
| 1 |
| 2 |
| 1 |
| 2 |
(2)解法一 由题意知
|
|

由图象知b+3c在点(0,-2)取到最小值-6,在点(0,0)处取到最大值0,
∴b+3c的最小值为-6,最大值为0;
解法二 由题意知
-1≤f(1)=1+b+c≤1,即-2≤b+c≤0,①
-1≤f(-1)=1-b+c≤1,即-2≤-b+c≤0,②
①×2+②得:-6≤2(b+c)+(-b+c)=b+3c≤0,
当b=0,c=-2时,b+3c=-6;当b=c=0,时,b+3c=0;
∴b+3c的最小值为-6,最大值为0;
解法三 由题意知
|
| f(1)-f(-1) |
| 2 |
| f(1)+f(-1)+2 |
| 2 |
∴b+3c=2f(1)+f(-1)-3,
∵-1≤f(-1)≤1,-1≤f(1)≤1,
∴-6≤b+3c≤0,
当b=0,c=-2时,b+3c=-6;当b=c=0,时,b+3c=0;
∴b+3c的最小值为-6,最大值为0;
(3)当n=2时,f(x)=x2+bx+c,对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,等价于在[-1,1]上最大值与最小值之差M≤4,据此分类讨论如下:
(i)当|
| b |
| 2 |
(ii)当-1≤-
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
(iii)当0≤-
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
综上所述,-2≤b≤2.
点评:本题考查函数恒成立问题,考查函数零点存在性定理的应用,考查线性规划的应用,也考查不等式的性质,考查绝对值的应用,渗透转化思想,方程思想,分类讨论思想,数形结合思想的考查,综合性极强,运算量大,难度高,属于难题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目