Question

（2012•陕西）设函数f(x)=

lnx，x＞0 -2x-1，x≤0

，D是由x轴和曲线y=f（x）及该曲线在点（1，0）处的切线所围成的封闭区域，则z=x-2y在D上的最大值为

2

．

Answer 1

分析：先求出曲线在点（1，0）处的切线，然后画出区域D，利用线性规划的方法求出目标函数z的最大值即可．

解答：解：当x＞0时，f′（x）=

1

x

则f′（1）=1所以曲线y=f（x）及该曲线在点（1，0）处的切线为y=x-1
D是由x轴和曲线y=f（x）及该曲线在点（1，0）处的切线所围成的封闭区域如下图阴影部分

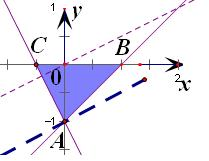
z=x-2y可变形成y=

1

2

x-

z

2

，当直线y=

1

2

x-

z

2

过点A（0，-1）时，截距最小，此时z最大
最大值为2
故答案为：2

点评：本题主要考查了线性规划，以及利用导数研究函数的切线，同时考查了作图的能力和分析求解的能力，属于中档题．