Question

【题目】已知以点 为圆心的圆与直线 相切，过点 的直线 与圆 相交于 两点， 是 的中点， .
（1）求圆 的标准方程；
（2）求直线 的方程.

Answer 1

【答案】
（1）解：设圆 的半径为 ，因为圆 与直线 相切，
∴ ，∴圆 的方程为
（2）解：①当直线 与 轴垂直时，易知 符合题意；
②当直线 与 轴不垂直时，设直线的方程为 ，即 ，
连接 ，则 ，∵ ，∴ ，
则由 得 ，∴直线 为： ，
故直线 的方程为 或 .
【解析】（1）利用点到直线的距离公式求出圆A的半径即可。
（2）分别就直线l是否与x轴垂直展开讨论。垂直时，易知 x = 2 符合题意；不垂直时，根据设出的l的方程表示出AQ后可以求出l的斜率，进而求出l的方程。
【考点精析】关于本题考查的一般式方程和点到直线的距离公式，需要了解直线的一般式方程：关于的二元一次方程（A，B不同时为0）；点到直线的距离为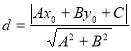：才能得出正确答案．