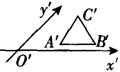题目内容
如图,已知△ABC的两边AB、AC的中点分别是M、N,在BN的延长线上取点P,使NP=BN,在CM的延长线上取点Q,使MQ=CM,求证:P、A、Q三点共线.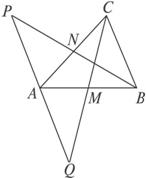
证明:设
=a,
=b,
∵M、N分别是
、
的中点,
∴
=2a,
=2b.
∴
=2b-2a,
=
+
=2b-2a+(-b)=b-2a,
=
+
=2a-2b-a=a-2b.
又N、M分别是BP、CQ的中点,
∴
=
=b-2a,
=
=a-2b.
∴
=
+
=2b-2a,
=
+
=2a-2b.
∴
=-
,从而
∥
.
又
与
都过点A,
∴A、P、Q三点共线.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知△ABC的面积为14，D、E分别为边AB、BC上的点，且AD：DB=BE：EC=2：1，AE与CD交于P．设存在λ和μ使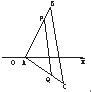
如图，已知△ABC的顶点坐标依次为A（1，0），B（5，8），C（7，-4），在边AB上有一点P，其横坐标为4，在AC上求一点Q，使线段PQ把△ABC分成面积相等的两部分．
如图，已知△ABC的顶点为A（2，4），B（0，-2），C（-2，3），求：
如图，已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D，以CD为直径的圆分别交BC，CA于点P、Q，求证：线段PQ平分△ABC的周长．
是边长为2的正三角形，则原△ABC的面积为__________.