题目内容
6. 如图,在三棱锥P-ABC中,BC⊥平面APC,AB=2$\sqrt{3}$,AP=PC=CB=2.
如图,在三棱锥P-ABC中,BC⊥平面APC,AB=2$\sqrt{3}$,AP=PC=CB=2.(1)求证:AP⊥平面PBC;
(2)求二面角P-AB-C的大小.
分析 (1)通过已知条件,可得AC2=PA2+PC2,进而可得AP⊥平面PBC;
(2)在平面APC内作PQ⊥AC于Q、过Q作QR⊥AB于R,连结PR,则∠PRQ即为二面角P-AB-C的平面角,计算即可.
解答 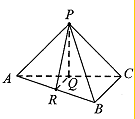 (1)证明:∵BC⊥平面APC,AC、AP?平面APC,
(1)证明:∵BC⊥平面APC,AC、AP?平面APC,
∴BC⊥AP,BC⊥AC,
∵AB=2$\sqrt{3}$,CB=2,∴AC=2$\sqrt{2}$,
又∵AP=PC=2,∴AC2=PA2+PC2,故AP⊥PC,
∵PC∩BC=C,∴AP⊥平面PBC;
(2)解:∵BC⊥平面APC,∴平面APC⊥平面ABC,
在平面APC内作PQ⊥AC于Q,则PQ⊥平面ABC,
过Q作QR⊥AB于R,连结PR,则∠PRQ即为二面角P-AB-C的平面角,
在RT△APC中,PQ=$\frac{AP•PC}{AC}=\sqrt{2}$,
在RT△ABC中,QR=$\frac{\sqrt{6}}{3}$,
故$tan∠PRQ=\frac{PQ}{QR}=\sqrt{3}$,
从而二面角P-AB-C的大小为$\frac{π}{3}$.
点评 本题考查线面垂直的判定定理,二面角的大小,注意解题方法的积累,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
15.第十二届《财富》全球论坛将于2013年6月在成都举行,为了使大会圆满举行,组委会在大学生中招聘了6名志愿者,其中甲大学有2名,乙大学有3名,丙大学有1名,若将他们安排在连续六天的服务工作中,每人一天,那么同一所大学的志愿者不安排在相邻两天服务的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{10}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{6}$ |
18.命题“?x∈R,x2-x+1>0”的否定是( )
| A. | ?x0∈R,x02-x0+1≤0 | B. | ?x0∈R,x02-x0+1≤0 | ||
| C. | ?x0R,x02-x0+1≤0 | D. | ?x0∈R,x02-x0+1≤0 |

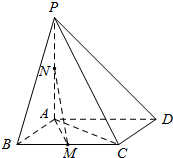 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.