Question

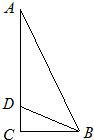如图，在Rt△ABC中，AC⊥BC，D在边AC上，已知BC=2，CD=1，∠ABD=45°，则AD=

 

．

Answer 1

分析：先设出AD=x，则AC可知，进而根据勾股定理可分别求得BD和AB，进而在△ABD中利用余弦定理建立方程求得x，则答案可得．

解答：解：设AD=x，则AC=1+x，BD=

4+1

=

5

AB=

4+(1+x) 2

由余弦定理可知cos45°=

BD2+AB2-AD2

2BD•AB

=

5+4+(1+x) 2-x2

2• 5 4+(1+x) 2

=

2

2

，整理得3x²-10x-25=0
解得x=5或-

5

3

（舍负）
故答案为：5

点评：本题主要考查了三角形的几何计算，余弦定理的应用．对于解三角形问题，要充分利用三角形中的边，角条件，灵活利用三角函数的基础知识，解决问题．