题目内容
若关于x的方程lnx-x-a=0恰有两个不同的实根，则实数a的取值范围是（ ）
| A、（-∞，-1] | B、（-∞，-1） | C、[-1，+∞） | D、（-1，+∞） |
分析：将方程 lnx-x-a=0恰有两个不同的实根，转化为一个函数y=lnx的图象与一条直线y=x+a的位置关系研究．
解答：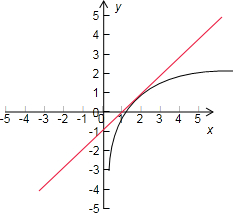
解：方程lnx-x-a=0化为：方程lnx=x+a
令 y=lnx，y=x+a
y=x+a表示过斜率为1的平行直线系
直线与曲线y=lnx相切时有a=-1，
k=-
若关于x的方程lnx-x-a=0恰有两个不同的实根，则实数a的取值范围是（-∞，-1）
故选B．
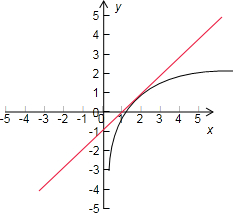解：方程lnx-x-a=0化为：方程lnx=x+a令 y=lnx，y=x+a
y=x+a表示过斜率为1的平行直线系
直线与曲线y=lnx相切时有a=-1，
k=-
| ||
| 3 |
若关于x的方程lnx-x-a=0恰有两个不同的实根，则实数a的取值范围是（-∞，-1）
故选B．
点评：本题主要考查根的存在性及根的个数判断，解答关键是利用直线与曲线的位置关系，要注意导数工具的应用和转化思想的应用．
练习册系列答案
金钥匙试卷系列答案
相关题目