题目内容
若关于x的方程lnx-ax=0只有一个实根,则实数a的范围是 .
【答案】分析:求导函数,分类讨论,确定函数的极值,讨论极值情况,即可得到结论.
解答:解:设f(x)=lnx-ax,定义域为(0,+∞),则f'(x)=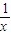 -a=0,可得x=
-a=0,可得x=
当a≤0,f'(x)>0,最多有一个实根,因为x>0,且x→0时,f(x)<0,f(1)≥0,所以(0,1]之间必有一个实根
a>0,0<x< 时,函数单调递增,x>
时,函数单调递增,x>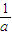 时,函数单调递减,f(
时,函数单调递减,f(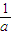 )=-lna-1为极大值,此极大值若为0的话,则有一个实根,此时a=
)=-lna-1为极大值,此极大值若为0的话,则有一个实根,此时a=
此极大值若大于0的话,会有两个实根,此极大值若小于0的话,则无实根.
因此a的取值范围为:(-∞,0]∪{ }
}
故答案为:(-∞,0]∪{ }.
}.
点评:本题利用导数解决方程根的个数问题,考查分类讨论的数学思想,属于中档题.
解答:解:设f(x)=lnx-ax,定义域为(0,+∞),则f'(x)=
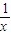 -a=0,可得x=
-a=0,可得x=
当a≤0,f'(x)>0,最多有一个实根,因为x>0,且x→0时,f(x)<0,f(1)≥0,所以(0,1]之间必有一个实根
a>0,0<x<
 时,函数单调递增,x>
时,函数单调递增,x>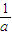 时,函数单调递减,f(
时,函数单调递减,f(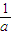 )=-lna-1为极大值,此极大值若为0的话,则有一个实根,此时a=
)=-lna-1为极大值,此极大值若为0的话,则有一个实根,此时a=
此极大值若大于0的话,会有两个实根,此极大值若小于0的话,则无实根.
因此a的取值范围为:(-∞,0]∪{
 }
}故答案为:(-∞,0]∪{
 }.
}.点评:本题利用导数解决方程根的个数问题,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
若关于x的方程lnx-x-a=0恰有两个不同的实根,则实数a的取值范围是( )
| A、(-∞,-1] | B、(-∞,-1) | C、[-1,+∞) | D、(-1,+∞) |