题目内容
已知函数f(x)=lnx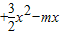
(Ⅰ)若函数f(x)图象上任意一点处的切线的倾斜角均不小于
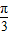 ,求实数m的取值范围;
,求实数m的取值范围;(Ⅱ)设m=2,若存在x∈[1,2],不等式|a+3x|-xf′(x)<0成立,求实数a的取值范围;
(III)已知k∈R,讨论关于x的方程f(x)+mx=
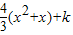 在区间[2,4]上的实根个数(e≈2.71828)
在区间[2,4]上的实根个数(e≈2.71828)
【答案】分析:(I)先求导函数,然后将函数f(x)图象上任意一点处的切线的倾斜角均不小于 转化成f′(x)≥tan
转化成f′(x)≥tan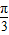 =
=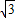 在(0,+∞)上恒成立,利用参数分离法可求出m的取值范围;
在(0,+∞)上恒成立,利用参数分离法可求出m的取值范围;
(II)根据绝对值不等式的性质化简不等式,然后利用参数分离法将a分离,最后利用存在性问题的常用方法进行求解即可;
(III)将k分离,然后利用导数研究函数的单调性,得到函数的最值,利用数形结合法可求出根的个数.
解答:解:(I)∵f(x)=lnx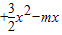 (x>0)
(x>0)
∴f′(x)=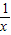 +3x-m
+3x-m
∵函数f(x)图象上任意一点处的切线的倾斜角均不小于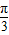 ,
,
∴f′(x)=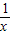 +3x-m≥tan
+3x-m≥tan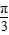 =
=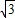 在(0,+∞)上恒成立
在(0,+∞)上恒成立
即m≤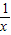 +3x-
+3x-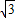 在(0,+∞)上恒成立,而
在(0,+∞)上恒成立,而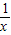 +3x-
+3x-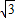 在(0,+∞)上的最小值为
在(0,+∞)上的最小值为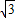
∴m≤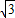
(II)当m=2时,f′(x)=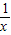 +3x-2
+3x-2
不等式|a+3x|-xf′(x)<0即为不等式|a+3x|-x(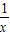 +3x-2)<0
+3x-2)<0
化简得不等式|a+3x|<3x2-2x+1
即-3x2+2x-1<a+3x<3x2-2x+1
∴存在x∈[1,2],使得不等式-3x2-x-1<a<3x2-5x+1成立
即(-3x2-x-1)min<a<(3x2-5x+1)max
即-15<a<3
(III)∵f(x)+mx=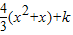
∴lnx+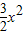 =
=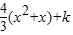
即k=lnx+ x2-
x2- x
x
令g(x)=lnx+ x2-
x2- x(x∈[2,4])
x(x∈[2,4])
则g′(x)=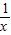 +
+ x-
x- =
=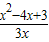 =
=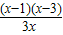
当x∈[2,3)时,g′(x)<0,当x∈(3,4]时,g′(x)>0
∴函数g(x)在[2,3)上单调递减,在(3,4)上单调递增
则当x=3时函数g(x)取最小值g(3)=ln3- ,而g(2)=ln2-2,g(4)=ln4-
,而g(2)=ln2-2,g(4)=ln4-
∴当k<ln3- 或k>ln4-
或k>ln4- 时方程f(x)+mx=
时方程f(x)+mx=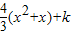 在区间[2,4]上的实根个数为0
在区间[2,4]上的实根个数为0
当k=ln3- 或ln2-2<k<ln4-
或ln2-2<k<ln4- 时方程f(x)+mx=
时方程f(x)+mx=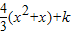 在区间[2,4]上的实根个数为1
在区间[2,4]上的实根个数为1
当ln3- <k≤ln2-2时方程f(x)+mx=
<k≤ln2-2时方程f(x)+mx=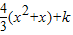 在区间[2,4]上的实根个数为2
在区间[2,4]上的实根个数为2
点评:本题主要考查了导数的几何意义,以及参数分离法研究恒成立和存在性问题,同时考查了运算求解的能力,属于中档题.
 转化成f′(x)≥tan
转化成f′(x)≥tan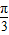 =
=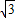 在(0,+∞)上恒成立,利用参数分离法可求出m的取值范围;
在(0,+∞)上恒成立,利用参数分离法可求出m的取值范围;(II)根据绝对值不等式的性质化简不等式,然后利用参数分离法将a分离,最后利用存在性问题的常用方法进行求解即可;
(III)将k分离,然后利用导数研究函数的单调性,得到函数的最值,利用数形结合法可求出根的个数.
解答:解:(I)∵f(x)=lnx
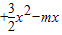 (x>0)
(x>0)∴f′(x)=
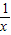 +3x-m
+3x-m∵函数f(x)图象上任意一点处的切线的倾斜角均不小于
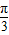 ,
,∴f′(x)=
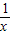 +3x-m≥tan
+3x-m≥tan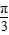 =
=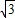 在(0,+∞)上恒成立
在(0,+∞)上恒成立即m≤
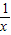 +3x-
+3x-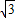 在(0,+∞)上恒成立,而
在(0,+∞)上恒成立,而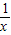 +3x-
+3x-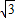 在(0,+∞)上的最小值为
在(0,+∞)上的最小值为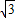
∴m≤
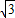
(II)当m=2时,f′(x)=
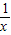 +3x-2
+3x-2不等式|a+3x|-xf′(x)<0即为不等式|a+3x|-x(
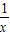 +3x-2)<0
+3x-2)<0化简得不等式|a+3x|<3x2-2x+1
即-3x2+2x-1<a+3x<3x2-2x+1
∴存在x∈[1,2],使得不等式-3x2-x-1<a<3x2-5x+1成立
即(-3x2-x-1)min<a<(3x2-5x+1)max
即-15<a<3
(III)∵f(x)+mx=
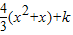
∴lnx+
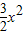 =
=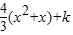
即k=lnx+
 x2-
x2- x
x令g(x)=lnx+
 x2-
x2- x(x∈[2,4])
x(x∈[2,4])则g′(x)=
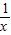 +
+ x-
x- =
=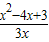 =
=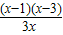
当x∈[2,3)时,g′(x)<0,当x∈(3,4]时,g′(x)>0
∴函数g(x)在[2,3)上单调递减,在(3,4)上单调递增
则当x=3时函数g(x)取最小值g(3)=ln3-
 ,而g(2)=ln2-2,g(4)=ln4-
,而g(2)=ln2-2,g(4)=ln4-
∴当k<ln3-
 或k>ln4-
或k>ln4- 时方程f(x)+mx=
时方程f(x)+mx=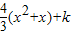 在区间[2,4]上的实根个数为0
在区间[2,4]上的实根个数为0当k=ln3-
 或ln2-2<k<ln4-
或ln2-2<k<ln4- 时方程f(x)+mx=
时方程f(x)+mx=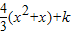 在区间[2,4]上的实根个数为1
在区间[2,4]上的实根个数为1当ln3-
 <k≤ln2-2时方程f(x)+mx=
<k≤ln2-2时方程f(x)+mx=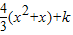 在区间[2,4]上的实根个数为2
在区间[2,4]上的实根个数为2点评:本题主要考查了导数的几何意义,以及参数分离法研究恒成立和存在性问题,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目